Blog Archives

Malware Counter Measure Standard Operation Procedure in Old Corporations

31/1/2021

featured image and summary — I have a few experience in playing around with cyber attacks, but it was merely a curiosity and I did this on my own PCs and virtual machines. Back then I tried exploiting the vulnerability on port 445 SMB using an exploit prepared by Metasploit. Metasploit also provided a tool to make backdoors (Trojan) which I practice after hijacking. The result was I can remotely control the victim's PC and after I activate the backdoor, I can connect whenever I want. Then after the vulnerability is patched (system updated) exploiting port 445 no longer works as explained on this lecture but for as long the backdoor is still implanted I can still remotely connect through there. If the vulnerability is exploited once and the system got infected by a virus, just patching it will not be enough. The infection must be healed. This is the fourth assignment from my Masters Advanced Network Security Course which has never been published anywhere and I, as the author and copyright holder, license this assignment customized CC-BY-SA where anyone can share, copy, republish, and sell on condition to state my name as the author and notify that the original and open version available here.

1. Cyber Attacks Can Come From Based on This Lecture

Kernel and server side of OS.
Application vulnerabilities.
Before and after infection of worm or virus.

Most famous attack is buffer overflow. PCs for file sharing are susceptible to remote buffer overflow. What happens if vulnerability is announced

With patch or update available.
No patch or update available.

The first case automatically or manually apply the patch. The second case disable the application or port that is vulnerable. Vulnerability can be:

Vulnerability due to design and programming error.
Vulnerability due to misconfiguration.
Vulnerability due to modules.

In case of design, the service must be disabled and reprogram. Case of misconfiguration, edit the configuration file, and as for modules disable and edit the module. To handle the vulnerabilities above the following common steps are taking.

Identify the vulnerability and plan the modification beforehand.
Isolate the system from the network.
Backup the system and make sure it can be restored.
It's suggested to perform simulation beforehand on similar environment, using virtual machine for example.
Finally perform modification. For beginners the step usually taken is update the system to the latest, after this process experts tends to manually modify. It's suggested to leave explanations on modified parts, for example leaving a comment on a configuration script that contain informations of what the modification is and when it was modified.

If not taking the steps above then there's a risked in rebuilding the system from the scratch since there's a chance in breaking the system when performing modification.

2. International Standard Organization Information Security Management

As written on the first part if it is already infected by a virus or worm then the infection must be cleaned. A software called antivirus had been developed which detects the infection based on patterns of the virus. By installing this software it can prevent and also clean the infections, but even this software is not perfect. If the antivirus cannot detect the infection then it's suggested to take the 5 steps above in dealing with the vulnerability. Worst case we must backup the data, destroy and rebuild the system.

The term “policy” is a set of rules and procedures that is agreed by involving parties, and then carried out. In my opinion the strategy build this information security policy must be carried out not in a hasty pace, because it includes parties that is not professional in IT and some are less aware of the cyber attacks that occurs. Even as a information security professional, if given a large book of the information security policy will respond as “this will take time to review”. So it is recommend to take it step by step as in some standards from International Standard Organization (ISO).

The first thing is to explain the current situation that many personal information is leaked, the network is swarming with worms and virus, and ultimately the damages cause a lost in profit of over millions of Yens. We should state as a national, if possible global crisis, or any other to convince that this is important.
Then create an overview of the important part of the security policy which includes the counter measures of the cyber attacks, for example what the system should be equipped with (antivirus, firewall, IDS, vulnerabilities patch, etc), and clearly separate private data and public data. Private data should not go into public data which we decided to be completely open, also measures to protect the private data should be stated for example the use of authorization and backup. Another important point that should be added is the procedure that should be taken if a threat is detected which in general it is isolating the PC from the network, reporting, then take action to fix the issue.
The first draft should only be the overview and contains only most important points, because this determines whether the policy be implemented or not. It's an important turning point and the strategy above is one of the best ways to open the door. When it's established then we can submit even more details of the security policy. For example security policy 2nd chapter should state about private informations, what data are important information, why is it important, and how's the impact if it's leaked, altered, or destroyed. 3nd chapter is about the system's equipment (what softwares should be installed, how the configuration should be, not to forget the physical secuirty as well, etc). 4Rd chapter of how to confront the network when holding private data, in other words our behavior that we should be careful when receiving attachments, suspicious files, dangerous site, and what we should do if we're attacked.

0 Comments

My Comments on Information Security Policy when I was a young student

28/1/2021

0 Comments

1. Kernel Vulnerabilities

kernel module — Design of the kernel itself.

Drivers embedded in the kernel.

The driver's module.

If it is the kernel design then we have no choice but to modify the whole system. The same applies if the driver is directly embedded in the kernel. If it is only the driver module then we can only focus on the module.

2. Server Program and CGI Vulnerabilities

server CGI — Program's and Common Gateway Interface (CGI)'s design.

Misconfiguration.

Problem on some modules.

For the design itself we must reprogram the whole thing. If it's due to misconfiguration for example allows code injections, and unintentionally leave an open port, we reconfigure the configuration usually by editing the configuration file. If there's problem on some modules then just focus on the modules.

3. Common Steps For Handling Previous Vulnerabilities

Identify the vulnerability and plan the modification beforehand.
Backup the system and make sure it can be restored.
It's suggested to perform simulation beforehand on similar environment, using virtual machine for example.
Finally perform modification. For beginners the step usually taken is update the system to the latest, after this process experts tends to manually modify. It's suggested to leave explanations on modified parts, for example leaving a comment on a configuration script that contain informations of what the modification is and when it was modified.

If not taking the steps above then there's a risked in rebuilding the system from the scratch since there's a chance in breaking the system when performing modification.

4. Some of My Comments and Experiences

My comment is that information security policy becomes necessary at the era of where we live know. As my first experience working at a corporation called Toshiba Tec, informations are very crucial. Just leaking a bit information outside the company can greatly damage both its image and income. There are informations that are highly classified that only the top management have authorization to access. Informations can be in form of physical substance (paper for example), but mostly today in form of electronics (word processor, spread sheet, image, video), that it is forbidden the use of hard drive on the companies private computer. With today's technology it is not unusual that access and exchanges of electronic information relies on computer networks.

In my company those in the information system division are responsible in handling the technology of electronic exchange at the same time the privacy of the exchange that informations must not leak outside of the company. They create a set of information security rule that was approved by the top managements of the company (a policy was created). To defend against outside threats, firewall, intrusion detection system, and antivirus were implemented. The networks were also strictly configure of who have the authentication to access. The division is also responsible to protect from the inside whether to prevent information leakage or to prevent information damage. In the policy is stated that employees are forbidden the use of outside electronic devices to connect to the network. A strict monitoring is installed on the IT infrastructure to record the time, and the person who access the information. Also the division is responsible in socializing the information security policy, especially of what both employers and employees are allowed to do and not do.

0 Comments

Dealing with Malware for Ordinary Users

28/1/2021

0 Comments

1. Mitigation

antivirus firewall update — This step is the most commonly used and mostly for those with the preference who are not expert in the area of malware. People usually know of the existence of malware and follows advices given by the media, experts, or computer companies to install firewalls, antivirus and antimalware softwares, and other preventive softwares. Finally tells them to update their Operating System (OS) (windows update for example), macrowares (word, spreadsheet), and other softwares to their latest version. Analogically equipped themselves with weapons and armors.

2. Evasion

beware of phisings — This step if you have better knowledge of malwares. Initially know the overview of how malwares works. (1) Like virus needs a host to run, resides on infected files, and can only initiate if you activate it. For this we will be careful when handling files by checking its size, its origin, its name, especially its format which virus resides in executeable formats. If it seems suspicious we should delete the file. If the system is modified, deleted, or a process occur without your approval is likely virus infected. (2) Other than virus a malware called worm exists, unlike virus it can infect a host without us executing it. In real life a worm can get inside of our body just getting contact in contaminated water. Virus cannot live without a host but worm can. In computer network is similar, even without your presence it keeps reproducing itself throught the network. Back then just by visiting a site or a mail server can already be infected with a worm. The network traffic could feel really heavy, or you might send informations to addresses you don't even recognize. If the site seems suspicious or receive a suspicious email, don't visit or open it. (3) Another dangerous malware that could take full control of your PC is a trojan horse. Back in the ancient Greeks this method was described as giving a large horse figure statue to the city of Troy during the Trojan war. Without any suspicion the city accepted the horse statue. What leads to the city's subjugation they didn't know there were soldiers inside the horse, and during the night those soldiers came out and took over the city. So in computers don't accept and execute suspicious files. (4) If already an expert, some says no need for antivirus. For example just use Linux or other OS other than Windows since most malwares are coded to attack Windows, using other system won't initiate the malware since the code doesn't match. This isn't everything and more measures are necessary.

3. Treatment

scan and safemode — if already infected then we have to treat the infection or remove it. First is identification to make sure if it really is an infection and it's not a hardware problem. When it is sure that is not hardware problem, identify the symptoms, whether the process is heavy, high memory consumption, heavy traffic, a program runs without your approval, etc. Don't forget to disconnect from the network (unless performing an online scan). For common people usually install an antivirus, perform a scan and clean. But this method is not guaranteed since it is perform on an infected host. The best way to do this is to get another clean PC with the latest software and antivirus update and perform a scan on the disk of the infected host. If you're really an expert then you can remove it manually by booting into safemode or input the disk into a different operating system, then delete the files and registries of the infection.

4. Last Resort

erase and reinstall — If all else fails the extreme resort is to destroy everything (along with the malware) and start again from a scratch. Reinstall your OS and have a fresh start (you may backup your data beforehand).

0 Comments

My Comments on Network and Bots and Pentest when I was a young student

27/1/2021

0 Comments

1. Network Consists of Clients and Servers

2. There Are Many Bots on The Network

hacker evolution bots — I have heard bot network before, I played a game called hacker evolution that gives a picture of bots but I never tried them before. If I were on the hacker side I will hijack into other clients PC using malware. That malware will inform back to me and I can use the hijacked clients to do something for me for example sending spam mails, or make new bot (find other victims). Usually as an amateur I would directly hack to the targeted server, but with this method is more effective because instead of using my own PC, I can use other PCs as well. I wonder if I can practice this in virtual machine. By the way some links on the buttom of the page are dead.

3. Popular Hacking Methods

ddos commview windows — DDOS or Denial of Service is very famous in hacking event among newcomers, which is to disable the service of a server. I have only practice this by flooding the traffic of a Wifi, the other I tried is on a server on client using many computer. The way I tried is very suitable using statement in number 2 using bots. By having many PC increases the computing power. About web defacement I have seen some sites have their contents hacked, either by modifying the contents or inserting new contents. Today there are many free tools available to scan for vulnerability, Nessus for example, and tools to exploit those vulnerability like Metasploit Framework. I'm only user of this tools so I still don't know the concept behind it. There also exist simple vulnerabilities due to misconfiguration for example MySQL injection that allows to use MySQL commands on login to bypass, or another one which I can modify the html page which allows to enter without password.

4. My Prior Knowledge About Penetration Testing

4 phases of pentest — In the past of learning network security the first thing I was asked to remember the OSI layers which consists of physical, datalink, network, transport, session, presentation, and application. Buffer overflow is very famous but the concept behind it for me is more tricky that others. I have read a book called The Basics of Hacking and Penetration Testing. The contents told me that there is a difference between hacker (black hat) for ill purposes and penetration tester (white hat) to find security holes in order to cover them. I on the other hand am a grey hat (only serve as a hobby and mere curiosity, and only finds satisfaction if able to hack a system and won't go further than that). Main the contents consist of 4 important steps of hacking which is highly recommend to follow in order. First and the most important part is information gathering which affect the outcomes of the other processes. Second is scanning, while information gathering gathers informations about the target, scanning scan this information like port scanning on certain found IP from information gathering. Then the third, the main step becomes affective which is exploitation. Finally the fourth is maintaining access for permanent access.

0 Comments

7,4 Hamming Codes

26/1/2021

0 Comments

0. Note

This is the fifth assignment from my Masters Applied Digital Information Theory Course which has never been published anywhere and I, as the author and copyright holder, license this assignment customized CC-BY-SA where anyone can share, copy, republish, and sell on condition to state my name as the author and notify that the original and open version available here.

1. Introduction

The previous 4th assignment demonstrate 1 bit error detection using 3,4 parity codes. On this assignment will be demonstrating 1 bit error correction using 7,4 hamming codes. On 3,4 parity codes we group 3 bits per block and perform exclusive or on each blocks to get a bit called the parity code bit and add it into the 4th bit of the blocks. A different approach for the 7,4 hamming codes we first group 4 bits per block, and then obtain the 3 hamming bit codes from the 4 bits for each blocks and add them which makes each blocks contained 7 bits. Suppose there are 4 bits as follows:

b1,b2,b3,b4

To get the hamming bit codes we do the following calculation:

b5=b1⊕b2⊕b3, b6=b1⊕b2⊕b4, b7=b1⊕b3⊕b4

Those bits will be added to the block:

b1,b2,b3,b4,b5,b6,b7

Following Table 1 are the complete list:

Table 1. Coding Table

Info	Code	Info	Code
0000	0000000	1000	1000110
0001	0001011	1001	1001101
0010	0010101	1010	1010011
0011	0011110	1011	1011000
0100	0100111	1100	1100001
0101	0101100	1101	1101010
0110	0110010	1110	1110100
0111	0111001	1111	1111111

On the receiver side the hamming codes is also constructed using the received first 4 bits of each blocks, then compare them with the hamming codes produced on the receiver side. Since the hamming codes were produced using the above equation (each codes uses different elements) we can know on which bit the error occurs, and a correction is performed. For example if receiver's b5, b6, b7 is different from transmitter's then an error on b1, if b5, b6 is different then an error occur on b2, if b5,b7 is different then an error occur on b3, if b6, b7 then b4, if b5 only then b5, if b6 only then b6, if b7 only then b7. Following Table 2 are the complete syndromes:

Table 2. Syndrome and Correction List

Syndrome	Correction	Syndrome	Correction	Syndrome	Correction	Syndrome	Correction
No error	None	b6 error	b6⊕1	b6b7 error	b4⊕1	b5b6 error	b2⊕1
b7 error	b7⊕1	b5 error	b5⊕1	b5b7 error	b3⊕1	all error	b1⊕1

2. Memoryless Errors (Skew Tent Map)

On this simulation we will (1) generate a chaotic binary sequence from memoryless source (2) perform hamming coding (3) simulate through a noisy channel (4) perform error correction on receiver. We will calculate the practical probabilities of incorrect decoding and compare them theoretically defined by P_I=1–P_C where P_C=7p(1-p)⁶ + (1-p)⁷ is the probability of correct decoding. The formula is derived from the probability of 1 bit error out of all possible error. Also we will compare the error probability of the binary sequence before correction and after correction. We will use critical point of c=0.499999 for generating the memoryless source, while we use c=1-p for generating the error sequence, and initial chaotic value for both is x(1)=0.333333 and various error probability p for the error sequence (noise). Generating the source will be the same as assignment 2, and generating the hamming codes is similar to 4th assignment except we input 3 extra bits in each blocks based on the initial 4 bits, which will make 7 bits. Like the previous assignment we perform exclusive or between the generated memoryless source and the error sequence to obtain the received sequence. On Table 3 is the simulation result of 1000000 (million) blocks (N) (7000000 bits) with error probability up to 0.4.

Table 3. simulation result of 1000000 (million) blocks (N) (7000000 bits) with error probability up to 0.4

Error Probability	0.01	0.05	0.1	0.2	0.3	0.4
Error Before Decoding	69185	310155	651846	1489329	2095701	2817931
Error After Decoding	5661	103819	413866	1456118	2253571	2871364
Probability Error Before Decoding	0.009884	0.044308	0.093121	0.212762	0.299386	0.402562
Probability Error After Decoding	0.008087	0.014831	0.059123	0.208017	0.321939	0.410195
Incorrect Decoding	1887	33173	132352	444091	672462	810696
Probability of Incorrect Decoding	0.001887	0.033173	0.132352	0.444091	0.672462	0.810696
Theoretical Probability of Incorrect Decoding	0.002031	0.044381	0.149695	0.423283	0.670583	0.841369

3. Markov-type Errors (PWL Map)

Similar to section 2 but this time we generate the error sequence through Markov type or Piece Wise Linear (PWL) map. The theoretical incorrect error decoding is P_I=1–P_C and correct one:

P_{C = P(1)p₂ (1-p)⁵ + 5P(0)p₁ p₂ (1-p₁)⁴ + P(0)(1-p₁)⁵ p₁ + P(0)(1-p₁)⁶}

We use the same critical point and initial chaotic value. To generate the error sequence we use the PWL map with various p2 values and P₁ = (1-c)/c P₂, with c=1-p. On Table 4 is the theoretical result of 1000000 (million) blocks (N) (7000000 bits) with error probability up to 0.4, Table 5 is the simulation result, Table 6 is error probability before decoding, Table 7 is error probability after decoding.

Table 4. Theoretical Result

p2\p	0.01	0.05	0.1	0.2	0.3	0.4
0.1	0.013497	0.067421	0.134663	0.268465	0.400994	0.531546
0.2	0.015996	0.079888	0.159498	0.317444	0.472536	0.622384
0.3	0.017509	0.087704	0.175712	0.351731	0.525154	0.690342
0.4	0.018048	0.091159	0.184430	0.375393	0.566651	0.746271

Table 5 Simulation Result

p2\p	0.01	0.05	0.1	0.2	0.3	0.4
0.1	0.014407	0.074791	0.165392	0.288812	0.409343	0.518025
0.2	0.039309	0.084100	0.125731	0.363730	0.463654	0.633573
0.3	0.013653	0.083021	0.179077	0.365025	0.567390	0.702815
0.4	0.011958	0.100293	0.248337	0.361628	0.607297	0.741535

Table 6. Error Probability Before Decoding

p2\p	0.01	0.05	0.1	0.2	0.3	0.4
0.1	0.019189	0.050632	0.121454	0.215809	0.310955	0.387244
0.2	0.0310312	0.050779	0.073711	0.239916	0.287656	0.390070
0.3	0.0064253	0.045953	0.095724	0.199656	0.351083	0.400005
0.4	0.0073853	0.051241	0.124822	0.196768	0.334634	0.393053

Table 7. Error Probability After Decoding

p2\p	0.01	0.05	0.1	0.2	0.3	0.4
0.1	0.0182	0.050889	0.120800	0.215805	0.311266	0.387078
0.2	0.0310312	0.050020	0.071017	0.236854	0.285676	0.395473
0.3	0.0065111	0.044599	0.095300	0.196479	0.336207	0.407214
0.4	0.0055779	0.050823	0.127047	0.189369	0.317022	0.398460

4. Results

On Figure 1 shows that the error probability before and after decoding fluctuates on different error probability values (p) and type of sources (memoryless and p2s), but had one thing in common that belowp < 0.3 the error after decoding decreases, and unfortunately rises above that. The incorrect coding for memoryless is preferable when p < 0.1 but not recommended when above. For PWL with p2=0.1 shows low incorrect decoding amongst other p2. For other values there is a cutting point on p=0.2, below lower p2 shows lower incorrect decoding and viceversa.

Figure 1. Error vs Error Before and After Decoding

5. Source Code

The source code is written in Fortran95 which is said to be a good programming language for mathematics in the old days, the first one is for memoryless, and the first one is for PWL (markov).

program Memoryless_Error_Hamming

! For safe purposes
 implicit none

! Type declarations
 integer :: m, n1, n2, i, j, s1, s2, s3
 real :: c, c_error, p, practical_error_before, p_practical_error_before, practical_error_after
 real :: p_practical_error_after, incorrect_decoding, p_incorrect_decoding
 real :: p_theory_correct_decoding, p_theory_incorrect_decoding
 real, dimension(40000000) :: x
 integer, dimension(40000000) :: bit
 integer, dimension(70000000) :: bit_hamming, bit_error, bit_receiver, bit_hamming_uncorrected, bit_corrected
 character(len=20) :: firstname, lastname, text
  
 write (*,'(A)',advance='no') 'Enter number of blocks: '
 read (*,*) m
 n1 = m*4
 n2 = m*7
 c = 0.499999

! Memoryless Generated Source (here n is number of bits)
 x(1) = 0.333333
 do i = 1, n1-1
  if (x(i) >= 0 .and. x(i) < c) then
   x(i+1) = x(i)/c
   bit(i) = 0
  else
   x(i+1) = (1-x(i))/(1-c)
   bit(i) = 1
  end if
 end do

! Hamming Codes
 j = 1
 do i = 1, n2, 7
  bit_hamming(i) = bit(j)
  bit_hamming(i+1) = bit(j+1)
  bit_hamming(i+2) = bit(j+2)
  bit_hamming(i+3) = bit(j+3)
  bit_hamming(i+4) = xor(xor(bit(j),bit(j+1)),bit(j+2))
  bit_hamming(i+5) = xor(xor(bit(j),bit(j+1)),bit(j+3))
  bit_hamming(i+6) = xor(xor(bit(j+1),bit(j+2)),bit(j+3))
  j = j+4
 end do

! Error Sequence
 write (*,'(A)',advance='no') 'Enter error probability: '
 read (*,*) p
 c_error = 1 - p
 do i = 1, n2
  if (x(i) >= 0 .and. x(i) < c_error) then
   x(i+1) = x(i)/c_error
   bit_error(i) = 0
  else
   x(i+1) = (1-x(i))/(1-c_error)
   bit_error(i) = 1
  end if
 end do

! Receiver Side (hamming encoded sequence + error sequence), calculate error probability before decoding, prefill future corrected bits
 practical_error_before = 0;
 do i = 1, n2
  bit_receiver(i) = xor(bit_hamming(i), bit_error(i))
  bit_corrected(i) = bit_receiver(i)
  if (bit_receiver(i) /= bit_hamming(i)) then
   practical_error_before = practical_error_before + 1
  end if
 end do
 p_practical_error_before = practical_error_before/n2
 
! Perform Hamming coding again on the received bits
 do i = 1, n2, 7
  bit_hamming_uncorrected(i) = bit_receiver(i)
  bit_hamming_uncorrected(i+1) = bit_receiver(i+1)
  bit_hamming_uncorrected(i+2) = bit_receiver(i+2)
  bit_hamming_uncorrected(i+3) = bit_receiver(i+3)
  bit_hamming_uncorrected(i+4) = xor(xor(bit_receiver(i),bit_receiver(i+1)),bit_receiver(i+2))
  bit_hamming_uncorrected(i+5) = xor(xor(bit_receiver(i),bit_receiver(i+1)),bit_receiver(i+3))
  bit_hamming_uncorrected(i+6) = xor(xor(bit_receiver(i+1),bit_receiver(i+2)),bit_receiver(i+3))
 end do

! Error Correction based on symptoms, "&" is placed to continue next line (fortran95 cannot read long lines)
 do i = 1, n2, 7
  if ((bit_hamming_uncorrected(i+4) /= bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) /= bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) /= bit_receiver(i+6))) then
   bit_corrected(i) = xor(bit_receiver(i),1)
  else if ((bit_hamming_uncorrected(i+4) /= bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) /= bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) == bit_receiver(i+6))) then
   bit_corrected(i+1) = xor(bit_receiver(i+1),1)
  else if ((bit_hamming_uncorrected(i+4) /= bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) == bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) /= bit_receiver(i+6))) then
   bit_corrected(i+2) = xor(bit_receiver(i+2),1)
  else if ((bit_hamming_uncorrected(i+4) == bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) /= bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) /= bit_receiver(i+6))) then
   bit_corrected(i+3) = xor(bit_receiver(i+3),1)
  else if ((bit_hamming_uncorrected(i+4) /= bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) == bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) == bit_receiver(i+6))) then
   bit_corrected(i+4) = xor(bit_receiver(i+4),1)
  else if ((bit_hamming_uncorrected(i+4) == bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) /= bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) == bit_receiver(i+6))) then
   bit_corrected(i+5) = xor(bit_receiver(i+5),1)
  else if ((bit_hamming_uncorrected(i+4) == bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) == bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) /= bit_receiver(i+6))) then
   bit_corrected(i+6) = xor(bit_receiver(i+6),1)  
  end if
 end do

! Error Probability After Decoding
 practical_error_after = 0;
 do i = 1, n2
  if (bit_corrected(i) /= bit_hamming(i)) then
   practical_error_after = practical_error_after + 1
  end if
 end do
 p_practical_error_after = practical_error_after/n2

! Probability of Correct, and incorrect decoding
 p_theory_correct_decoding = (7*p*(1-p)*(1-p)*(1-p)*(1-p)*(1-p)*(1-p))+((1-p)*(1-p)*(1-p)*(1-p)*(1-p)*(1-p)*(1-p))
 p_theory_incorrect_decoding = 1 - p_theory_correct_decoding
 incorrect_decoding = 0
 do i = 1, n2, 7
  if ((bit_corrected(i) /= bit_hamming(i)) .or. (bit_corrected(i+1) /= bit_hamming(i+1)) .or. &
(bit_corrected(i+2) /= bit_hamming(i+2)) .or. (bit_corrected(i+3) /= bit_hamming(i+3)) .or. &
(bit_corrected(i+4) /= bit_hamming(i+4)) .or. (bit_corrected(i+5) /= bit_hamming(i+5)) .or. &
(bit_corrected(i+6) /= bit_hamming(i+6))) then
   incorrect_decoding = incorrect_decoding + 1
  end if
 end do
 p_incorrect_decoding = incorrect_decoding/m

! Results
 write (*,'(A)',advance='no') 'Practical error before decoding: '
 write (*,*) practical_error_before
 write (*,'(A)',advance='no') 'Practical error after decoding: '
 write (*,*) practical_error_after
 write (*,'(A)',advance='no') 'Probability practical error before decoding: '
 write (*,*) p_practical_error_before
 write (*,'(A)',advance='no') 'Probability practical error after decoding: '
 write (*,*) p_practical_error_after
 write (*,'(A)',advance='no') 'Incorrect decoding: '
 write (*,*) incorrect_decoding
 write (*,'(A)',advance='no') 'Probability of incorrect decoding: '
 write (*,*) p_incorrect_decoding
 write (*,'(A)',advance='no') 'Theoretical probability of incorrect decoding: '
 write (*,*) p_theory_incorrect_decoding


! Debugging purposes, uncomment them to see binary sequences, max 18 blocks
! do i = 1, n2
!  write(*,'(1i1.1)',advance='no') bit_hamming(i)
! end do
! write (*,*) ' '
! do i = 1, n2
!  write(*,'(1i1.1)',advance='no') bit_error(i)
! end do
! write (*,*) ' '
! do i = 1, n2
!  write(*,'(1i1.1)',advance='no') bit_receiver(i)
! end do
!  write (*,*) ' '
!  do i = 1, n2
!  write(*,'(1i1.1)',advance='no') bit_corrected(i)
! end do
!  write (*,*) ' '

end program Memoryless_Error_Hamming

program Piece_Wise_Linear_Error

! For safe purposes
 implicit none

! Type declarations
 integer :: m, n1, n2, i, j, s1, s2, s3
 real :: c, c_error, p, practical_error_before, p_practical_error_before, practical_error_after
 real :: p_practical_error_after, incorrect_decoding, p_incorrect_decoding
 real :: p_theory_correct_decoding, p_theory_incorrect_decoding
 real :: p1, p2, a, a1, a2, a3, c1, c2, d1, d2
 real, dimension(40000000) :: x
 integer, dimension(40000000) :: bit
 integer, dimension(70000000) :: bit_hamming, bit_error, bit_receiver, bit_hamming_uncorrected, bit_corrected
 character(len=20) :: firstname, lastname, text
  
 write (*,'(A)',advance='no') 'Enter number of blocks: '
 read (*,*) m
 n1 = m*4
 n2 = m*7
 c = 0.499999
 x(1) = 0.333333

! Uncomment to use memoryless source
! Memoryless Generated Source (here n is number of bits)
! x(1) = 0.333333
! do i = 1, n1-1
!  if (x(i) >= 0 .and. x(i) < c) then
!   x(i+1) = x(i)/c
!   bit(i) = 0
!  else
!   x(i+1) = (1-x(i))/(1-c)
!   bit(i) = 1
!  end if
! end do

! PWL Generated Source
 p1 = (1-c)*p2/c
 a = 1/(1-(p1+p2))
 if (p1+p2 < 1) then
  c1 = c-(c/a)
  c2 = c+((1-c)/a)
  d1 = c1*(1-c)
  d2 = 1-((1-c2)*c)
  a1 = -c/(c1-d1)
  a2 = a
  a3 = (c-1)/(d2-c2)
  do i = 1, n2
   if (x(i) >= 0 .and. x(i) < c1) then
    x(i+1) = (a1*(x(i)-d1))+c
   else if (x(i) >= c1 .and. x(i) < c2) then
    x(i+1) = a2*(x(i)-c1)
   else
    x(i+1) = (a3*(x(i)-c2))+1
   end if
   if (x(i) >= 0 .and. x(i) < c) then
    bit(i) = 0
   else
    bit(i) = 1
   end if
  end do
 else
  c1 = c-((c-1)/a)
  c2 = c-(c/a)
  d1 = c1*(1-c)
  d2 = 1-((1-c2)*(1-c))
  a1 = -c/(c1-d1)
  a2 = a
  a3 = c/(d2-c2)
  do i = 1, n2
   if (x(i) >= 0 .and. x(i) < c1) then
    x(i+1) = (a1*(x(i)-d1))+c
   else if (x(i) >= c1 .and. x(i) < c2) then
    x(i+1) = (a2*(x(i)-c1))+1
   else
    x(i+1) = a3*(x(i)-c2)
   end if
   if (x(i) >= 0 .and. x(i) < c) then
    bit(i) = 0
   else
    bit(i) = 1
   end if
  end do
 end if

! Hamming Codes
 j = 1
 do i = 1, n2, 7
  bit_hamming(i) = bit(j)
  bit_hamming(i+1) = bit(j+1)
  bit_hamming(i+2) = bit(j+2)
  bit_hamming(i+3) = bit(j+3)
  bit_hamming(i+4) = xor(xor(bit(j),bit(j+1)),bit(j+2))
  bit_hamming(i+5) = xor(xor(bit(j),bit(j+1)),bit(j+3))
  bit_hamming(i+6) = xor(xor(bit(j+1),bit(j+2)),bit(j+3))
  j = j+4
 end do

! Error Sequence
 write (*,'(A)',advance='no') 'Enter error probability: '
 read (*,*) p
 c_error = 1 - p
 write (*,'(A)',advance='no') 'Enter p2: '
 read (*,*) p2
 p1 = (1-c_error)*p2/c_error
 a = 1/(1-(p1+p2))
 if (p1+p2 < 1) then
  c1 = c_error-(c_error/a)
  c2 = c_error+((1-c_error)/a)
  d1 = c1*(1-c_error)
  d2 = 1-((1-c2)*c_error)
  a1 = -c_error/(c1-d1)
  a2 = a
  a3 = (c_error-1)/(d2-c2)
  do i = 1, n2
   if (x(i) >= 0 .and. x(i) < c1) then
    x(i+1) = (a1*(x(i)-d1))+c_error
   else if (x(i) >= c1 .and. x(i) < c2) then
    x(i+1) = a2*(x(i)-c1)
   else
    x(i+1) = (a3*(x(i)-c2))+1
   end if
   if (x(i) >= 0 .and. x(i) < c_error) then
    bit_error(i) = 0
   else
    bit_error(i) = 1
   end if
  end do
 else
  c1 = c_error-((c_error-1)/a)
  c2 = c_error-(c_error/a)
  d1 = c1*(1-c_error)
  d2 = 1-((1-c2)*(1-c_error))
  a1 = -c_error/(c1-d1)
  a2 = a
  a3 = c_error/(d2-c2)
  do i = 1, n2
   if (x(i) >= 0 .and. x(i) < c1) then
    x(i+1) = (a1*(x(i)-d1))+c_error
   else if (x(i) >= c1 .and. x(i) < c2) then
    x(i+1) = (a2*(x(i)-c1))+1
   else
    x(i+1) = a3*(x(i)-c2)
   end if
   if (x(i) >= 0 .and. x(i) < c_error) then
    bit_error(i) = 0
   else
    bit_error(i) = 1
   end if
  end do
 end if

! Receiver Side (hamming encoded sequence + error sequence), calculate error probability before decoding, prefill future corrected bits
 practical_error_before = 0;
 do i = 1, n2
  bit_receiver(i) = xor(bit_hamming(i), bit_error(i))
  bit_corrected(i) = bit_receiver(i)
  if (bit_receiver(i) /= bit_hamming(i)) then
   practical_error_before = practical_error_before + 1
  end if
 end do
 p_practical_error_before = practical_error_before/n2
 
! Perform Hamming coding again on the received bits
  
 do i = 1, n2, 7
  bit_hamming_uncorrected(i) = bit_receiver(i)
  bit_hamming_uncorrected(i+1) = bit_receiver(i+1)
  bit_hamming_uncorrected(i+2) = bit_receiver(i+2)
  bit_hamming_uncorrected(i+3) = bit_receiver(i+3)
  bit_hamming_uncorrected(i+4) = xor(xor(bit_receiver(i),bit_receiver(i+1)),bit_receiver(i+2))
  bit_hamming_uncorrected(i+5) = xor(xor(bit_receiver(i),bit_receiver(i+1)),bit_receiver(i+3))
  bit_hamming_uncorrected(i+6) = xor(xor(bit_receiver(i+1),bit_receiver(i+2)),bit_receiver(i+3))
 end do

! Error Correction based on symptoms, "&" is placed to continue next line (fortran95 cannot read long lines)
 do i = 1, n2, 7
  if ((bit_hamming_uncorrected(i+4) /= bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) /= bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) /= bit_receiver(i+6))) then
   bit_corrected(i) = xor(bit_receiver(i),1)
  else if ((bit_hamming_uncorrected(i+4) /= bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) /= bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) == bit_receiver(i+6))) then
   bit_corrected(i+1) = xor(bit_receiver(i+1),1)
  else if ((bit_hamming_uncorrected(i+4) /= bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) == bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) /= bit_receiver(i+6))) then
   bit_corrected(i+2) = xor(bit_receiver(i+2),1)
  else if ((bit_hamming_uncorrected(i+4) == bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) /= bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) /= bit_receiver(i+6))) then
   bit_corrected(i+3) = xor(bit_receiver(i+3),1)
  else if ((bit_hamming_uncorrected(i+4) /= bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) == bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) == bit_receiver(i+6))) then
   bit_corrected(i+4) = xor(bit_receiver(i+4),1)
  else if ((bit_hamming_uncorrected(i+4) == bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) /= bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) == bit_receiver(i+6))) then
   bit_corrected(i+5) = xor(bit_receiver(i+5),1)
  else if ((bit_hamming_uncorrected(i+4) == bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) == bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) /= bit_receiver(i+6))) then
   bit_corrected(i+6) = xor(bit_receiver(i+6),1)  
  end if
 end do

! Error Probability After Decoding
 practical_error_after = 0;
 do i = 1, n2
  if (bit_corrected(i) /= bit_hamming(i)) then
   practical_error_after = practical_error_after + 1
  end if
 end do
 p_practical_error_after = practical_error_after/n2

! Probability of Correct, and incorrect decoding
 p_theory_correct_decoding = (((1-c_error)*p2*((1-p1)**5)) + (5*c_error*p1*p2*((1-p1)**4)) + (c_error*((1-p1)**5)*p1) + &
(c_error*((1-p1)**6)))
 p_theory_incorrect_decoding = 1 - p_theory_correct_decoding
 incorrect_decoding = 0
 do i = 1, n2, 7
  if ((bit_corrected(i) /= bit_hamming(i)) .or. (bit_corrected(i+1) /= bit_hamming(i+1)) .or. &
(bit_corrected(i+2) /= bit_hamming(i+2)) .or. (bit_corrected(i+3) /= bit_hamming(i+3)) .or. &
(bit_corrected(i+4) /= bit_hamming(i+4)) .or. (bit_corrected(i+5) /= bit_hamming(i+5)) .or. &
(bit_corrected(i+6) /= bit_hamming(i+6))) then
   incorrect_decoding = incorrect_decoding + 1
  end if
 end do
 p_incorrect_decoding = incorrect_decoding/m

! Results
 write (*,'(A)',advance='no') 'Practical error before decoding: '
 write (*,*) practical_error_before
 write (*,'(A)',advance='no') 'Practical error after decoding: '
 write (*,*) practical_error_after
 write (*,'(A)',advance='no') 'Probability practical error before decoding: '
 write (*,*) p_practical_error_before
 write (*,'(A)',advance='no') 'Probability practical error after decoding: '
 write (*,*) p_practical_error_after
 write (*,'(A)',advance='no') 'Incorrect decoding: '
 write (*,*) incorrect_decoding
 write (*,'(A)',advance='no') 'Probability of incorrect decoding: '
 write (*,*) p_incorrect_decoding
 write (*,'(A)',advance='no') 'Theoretical probability of incorrect decoding: '
 write (*,*) p_theory_incorrect_decoding


! Debugging purposes, uncomment them to see binary sequences, max 18 blocks
! do i = 1, n2
!  write(*,'(1i1.1)',advance='no') bit_hamming(i)
! end do
! write (*,*) ' '
! do i = 1, n2
!  write(*,'(1i1.1)',advance='no') bit_error(i)
! end do
! write (*,*) ' '
! do i = 1, n2
!  write(*,'(1i1.1)',advance='no') bit_receiver(i)
! end do
!  write (*,*) ' '
!  do i = 1, n2
!  write(*,'(1i1.1)',advance='no') bit_corrected(i)
! end do
!  write (*,*) ' '

end program Piece_Wise_Linear_Error

0 Comments

(4,3)-Single Parity Check of Binary Sequence Skew Tent and PWL Map

25/1/2021

0 Comments

0. Note

This is the fourth assignment from my Masters Applied Digital Information Theory Course which has never been published anywhere and I, as the author and copyright holder, license this assignment customized CC-BY-SA where anyone can share, copy, republish, and sell on condition to state my name as the author and notify that the original and open version available here.

1. Introduction

On Figure 1 of Shannon Communication Model, the previous assignments on memoryless and Markov's source is on the first block transmitter (source), while this fourth assignment is on the channel coding and decoding. It will be demonstrated a binary source coded with parity check codes , going through a noisy channel with the specified bit error rate, and decoded on with parity check. On the receiver side will compare the theoretical and practical error using parity check.

A parity (3,4) check coding takes 3 bits + 1 into 1 block with the last bit as the parity bit obtained by performing exclusive or (xor) on the 3 bits. The blocks are then transmitted and xor is again performed on the decoder side on the 4 bits of the block, and if the result is 0 then it's not regarded as error, but if the result is 1 then it's regarded as error. Looking this checking method it can detect errors when odd numbers of bits error occurs, but it cannot detect when even number of error occurs. This can be demonstrated on the following table.

Table 1. Parity Check Examples

Information	110	100	101
Code Words	1100 (1⊕1⊕0→0)	1001 (1⊕0⊕0→1)	1010 (1⊕0⊕1→0)
Errors	0000	0100	0011
Received	1100 (1100⊕0000)	1101 (1001⊕0100)	1001 (1010⊕0011)
Judgement	1⊕1⊕0⊕0=0 (no error) correct	1⊕1⊕0⊕1=1 (error) correct	1⊕0⊕0⊕1=0 (no error) wrong

2. Skew Tent Map

The binary sequence on the transmitter is generated by means of 2nd assignment of skew tent map with initial x[1] = 0.1 and c = 0.499999. This time we generated in a million blocks with each blocks contains 3 + 1 bits. On the source we generated the initial bits of normal means on assignment 2, but then we slip a parity bit on every 4th increments of the sequence (on the actual code we made 2 sequence where the first sequence as a reference for the sequence with parity bit, b2[0] = b1[0], b2[1] = b1[1], b2[2] = b1[2], b2[3] = b1[0]⊕b1[1]⊕b1[2], b2[4] = b1[3], b2[5] = b1[4], b2[6] = b1[5], b2[7] = b1[3]⊕b1[4]⊕b1[5], and so on).

After that we simulate an error sequence with initial x_err[0] = 0.500001, error probability p varies, and c_err = 1-p. Then as per section 1 we xor the parity coded binary sequence with the error simulated generated sequence, obtaining the binary sequence at the receiver. We can find the total errors by comparing the binary sequence on the transmitter side (before xor by error sequence) and on the receiver side (after xor by error sequence). Then we perform xor on each blocks (every 4 bits) of the receiver binary sequence to get the detected error. Finally we calculate the difference between total errors (real) and detected error to find the practical undetected error. The theoretical undetected error can be calculated using the following equation: P_u = 6p²(1-p)²+p⁴ which is actually a formula of the probability of even blocks after passing through noisy channel with defined error probability.

Table 2. Trials of Error Probability to Undetected Error

p	0.01	0.05	0.1	0.24	0.49	0.73
Total Error	39348	185428	344862	653470	934984	997957
Detected Error	39167	171220	295457	445080	497971	500982
Undetected Error	181	14208	49405	208390	437013	496975
P Total Error	0.039348	0.185428	0.344862	0.65347	0.934984	0.997957
P Detected Error	0.039167	0.17122	0.295457	0.44508	0.497971	0.500982
P UndetectedError	0.000181	0.014208	0.049405	0.20839	0.437013	0.496975
P UndetectedError Theory	0.00058807	0.0135438	0.0487	0.202936	0.432348	0.517073

3. PWL Map

Roughly similar to 2nd section but this time use PWL Map error sequence. We start by choosing p2, but generating the error sequence we defined c_err as 1-p (initial c remain 0.499999 and p1 is computed), with p2 still the same, but p1_err is defined based on c_err. Automatically slop a changes and the sequence was generated. The process is the same after that, with the theoretical of undetected error as Pu = P(0)((1-p1)p1(1-p2)+p1(1-p2)p2+p1p2p1) + p(1)(p2(1-p1)p1+p2p1p2+(1-p2)p2(1-p1)+(1-p2)(1-p2)(1-p2)), again is actually a formula of even blocks probability after passing through noisy channel with defined error probability.

Table 3. Probability of Practical Undetected Error of different values of p to values of p2

p2\p	0.01	0.05	0.1	0.24	0.49	0.73
0.2	0.028872	0.039856	0.075678	0.187323	0.429819	0.575357
0.4	0.005627	0.040695	0.076027	0.178473	0.40059	0.491026
0.6	0.005245	0.030903	0.07767	0.202801	0.474428	-
0.8	0.000957	0.0247	0.059482	0.202483	0.653459	-

Table 4. Probability of Theoretical Undetected Error of different values of p to values of p2

p2\p	0.01	0.05	0.1	0.24	0.49	0.73
0.2	0.00863918	0.0431779	0.0863013	0.206562	0.415975	0.57224
0.4	0.00792962	0.0398438	0.0801877	0.195824	0.404327	0.426112
0.6	0.00693068	0.0356964	0.0741334	0.198148	0.476694	-
0.8	0.0047017	0.0264344	0.0606124	0.203898	0.654715	-

4. Summary

From above the practical value almost matches the theoretical value. As on Figure 2 plotted based on tables above, for error probability below 0.2 the skew tent map has lower undetected error probability which good to use on channels with little noise. For above it's better to use PWL but with p2 value lower than 0.5.

Figure 2. Probability Error vs Undetected Error Probability

5. Source Code

The source code is divided into 2 one for skew tent map and the other for PWL map written in C++.

//============================================================================
// Name        : skew-tent-map.cpp
// Author      : Fajar Purnama 152-D8713
// Version     : 0.9
// Copyright   : Free to distributed with credits to the author.
// Description : Source Code for Skew Tent Map in C++
//============================================================================

#include <iostream>
using namespace std;

int main() {
        cout << "!!!Hello World!!!" << endl; // prints !!!Hello World!!!

        int N = 10000*3, bin[N]; float x[N], c = 0.499999; x[0] = 0.3;
        // N = number of bits (1 block = 3 bits), c = critical point, x[0] = initial value, x[N] = chaotic sequence, and bin[N] = binary sequence

        // From here is 2nd Assignment
        for (int i = 0; i < N; ++i){
                if (x[i] >= 0 && x[i] < c) {
                        x[i+1] = x[i]/c;
                        bin[i] = 0;
                } else {
                        x[i+1] = (1-x[i])/(1-c);
                        bin[i] = 1;
                }
        }
        // Insert bit parity on every 4th bit
        int j = 0, bin_par[N+(N/3)];
        for (int i = 0; i < N+(N/3); i += 4){
                bin_par[i] = bin[j];
                bin_par[i+1] = bin[j+1];
                bin_par[i+2] = bin[j+2];
                bin_par[i+3] = bin_par[i]^bin_par[i+1]^bin_par[i+2];
                j += 3;
        }

        // Generate error sequence
        int bin_err[N+(N/3)]; float p;
        cout << "Enter error probability: "; cin >> p;
        float c_err = 1-p, x_err[N+(N/3)]; x_err[0]=0.500001;
        for (int i = 0; i < N+(N/3); ++i){
                if (x_err[i] >= 0 && x_err[i] < c_err) {
                        x_err[i+1] = x_err[i]/c_err;
                        bin_err[i] = 0;
                } else {
                        x_err[i+1] = (1-x_err[i])/(1-c_err);
                        bin_err[i] = 1;
                }
        }

        // Generate receiver side = parity sequence XOR error sequence
        int bin_r[N+(N/3)];
        for (int i = 0; i < N+(N/3); ++i){
                bin_r[i] = bin_par[i] ^ bin_err[i];
        }

        for (int i = 0; i < N+(N/3); ++i){
                cout << bin_err[i];
        }
        cout << endl;
        for (int i = 0; i < N+(N/3); ++i){
                cout << bin_par[i];
        }
        cout << endl;
        for (int i = 0; i < N+(N/3); ++i){
                cout << bin_r[i];
        }
        cout << endl << endl;
        // total error, detected error, undetected error
        float total_error = 0, detected_error = 0, undetected_error = 0;
        float p_theory = ((6*p*p)*((1-p)*(1-p))+(p*p*p*p));
        for (int i = 0; i < N+(N/3); i += 4){
                if((bin_par[i] != bin_r[i])||(bin_par[i+1] != bin_r[i+1])||(bin_par[i+2] != bin_r[i+2])||(bin_par[i+3] != bin_r[i+3])){
                        ++total_error;
                }
                if((bin_r[i]^bin_r[i+1]^bin_r[i+2]^bin_r[i+3])==1){
                        ++detected_error;
                }
        }
        undetected_error = total_error - detected_error;
        float p_total_error = total_error/(N/3);
        float p_detected_error = detected_error/(N/3);
        float p_undetected_error = undetected_error/(N/3);
        cout << "total error = " << total_error << endl;
        cout << "detected error = " << detected_error << endl;
    cout << endl;
        cout << "undetected error = " << undetected_error << endl;
        cout << "probability of total error = " << p_total_error << endl;
        cout << "probability of detected error = " << p_detected_error << endl;
        cout << "probability of undetected error = " << p_undetected_error << endl;
        cout << "theory = " << p_theory << endl;
        return 0;
}

//============================================================================
// Name        : 43-single-parity-check-codes-large.cpp
// Author      : Fajar Purnama 152-D8713
// Version     : 0.9
// Copyright   : Free to distributed with credits to the author.
// Description : Source Code for PWL Tent Map in C++
//============================================================================

#include <iostream>
using namespace std;

int main() {
        int n;
        cout << "Enter number of blocks: "; cin >> n;
        int N = n*3; float p1, p2, c, c1, c2, d1, d2, a, a1, a2, a3;
        c = 0.499999; cout << "Enter value of p2: "; cin >> p2;
        p1 = (1-c)*p2/c;
        a = 1/(1-(p1+p2));
        int* bin = new int[N]; // need to do this because int main cannot hold large numbers, a stack overflow occurs so need to allocate to new heap
        float* x = new float[N]; x[0] = 0.1;
        // N = number of bits (1 block = 3 bits), c = critical point, x[0] = initial value, x[N] = chaotic sequence, and bin[N] = binary sequence

        // From here is 3rd Assignment
        if (p1+p2 < 1){
        
        c1 = c-(c/a);
        c2 = c+((1-c)/a );
        d1 = c1*(1-c);
        d2 = 1-((1-c2)*c);

        a1 = -c/(c1-d1);
        a2 = a;
        a3 = (c-1)/(d2-c2);

        for (int i = 0; i < N; ++i){
                if (x[i] >= 0 && x[i] < c1) {
                        x[i+1] = (a1*(x[i]-d1))+c;
                } else if(x[i] >= c1 && x[i] < c2) {
                        x[i+1] = a2*(x[i]-c1);
                } else {
                        x[i+1] = (a3*(x[i]-c2))+1;
                }
                if (x[i] < c){
                        bin[i] = 0;
                } else {
                        bin[i] = 1;
                }
        }
        } else if (p1+p2 > 1){
        
        c1 = c-((c-1)/a);
        c2 = c-(c/a);

        d1 = c1*(1-c);
        d2 = 1-((1-c2)*(1-c));

        a1 = -c/(c1-d1);
        a2 = a;
        a3 = c/(d2-c2);

        for (int i = 0; i < N; ++i){
                if (x[i] >= 0 && x[i] < c1) {
                        x[i+1] = (a1*(x[i]-d1))+c;
                } else if(x[i] >= c1 && x[i] < c2) {
                        x[i+1] = (a2*(x[i]-c1))+1;
                } else {
                        x[i+1] = a3*(x[i]-c2);
                }
                if (x[i] < c){
                        bin[i] = 0;
                } else {
                        bin[i] = 1;
                }
        }
        } else {
                cout << "you can't do this" << endl;
        }

        // Insert bit parity on every 4th bit
        int j = 0; int* bin_par = new int[N+(N/3)];
        for (int i = 0; i < N+(N/3); i += 4){
                bin_par[i] = bin[j];
                bin_par[i+1] = bin[j+1];
                bin_par[i+2] = bin[j+2];
                bin_par[i+3] = bin_par[i]^bin_par[i+1]^bin_par[i+2];
                j += 3;
        }

        // Generate error sequence
        int* bin_err = new int[N+(N/3)]; float p, p1_err;
        float* x_err = new float[N+(N/3)]; x_err[0]=x[0];
        cout << "Enter error probability :"; cin >> p;
        float c_err = 1-p;
        p1_err = (1-c_err)*p2/c_err;
        a = 1/(1-(p1_err+p2));

        if (p1_err+p2 < 1){
        
        c1 = c_err-(c_err/a);
        c2 = c_err+((1-c_err)/a );
        d1 = c1*(1-c_err);
        d2 = 1-((1-c2)*c_err);

        a1 = -c_err/(c1-d1);
        a2 = a;
        a3 = (c_err-1)/(d2-c2);

        for (int i = 0; i < N+(N/3); ++i){
                if (x_err[i] >= 0 && x_err[i] < c1) {
                        x_err[i+1] = (a1*(x_err[i]-d1))+c_err;
                } else if(x_err[i] >= c1 && x_err[i] < c2) {
                        x_err[i+1] = a2*(x_err[i]-c1);
                } else {
                        x_err[i+1] = (a3*(x_err[i]-c2))+1;
                }
                if (x_err[i] < c_err){
                        bin_err[i] = 0;
                } else {
                        bin_err[i] = 1;
                }
        }
        } else if (p1_err+p2 > 1){
        
        c1 = c_err-((c_err-1)/a);
        c2 = c_err-(c_err/a);

        d1 = c1*(1-c_err);
        d2 = 1-((1-c2)*(1-c_err));

        a1 = -c_err/(c1-d1);
        a2 = a;
        a3 = c_err/(d2-c2);

        for (int i = 0; i < N+(N/3); ++i){
                if (x_err[i] >= 0 && x_err[i] < c1) {
                        x_err[i+1] = (a1*(x_err[i]-d1))+c_err;
                } else if(x_err[i] >= c1 && x_err[i] < c2) {
                        x_err[i+1] = (a2*(x_err[i]-c1))+1;
                } else {
                        x_err[i+1] = a3*(x_err[i]-c2);
                }
                if (x_err[i] < c_err){
                        bin_err[i] = 0;
                } else {
                        bin_err[i] = 1;
                }
        }
        } else {
                cout << "you can't do this" << endl;
        }

        // Generate receiver side = parity sequence XOR error sequence
        int* bin_r = new int[N+(N/3)];
        for (int i = 0; i < N+(N/3); ++i){
                bin_r[i] = bin_par[i] ^ bin_err[i];
        }
 
       /* Debugging Purpose
   for (int i = 0; i < N+(N/3); ++i){
           cout << bin_err[i];
   }
   cout << endl;
   for (int i = 0; i < N+(N/3); ++i){
           cout << bin_par[i];
   }
   cout << endl;
   for (int i = 0; i < N+(N/3); ++i){
           cout << bin_r[i];
   }
   cout << endl << endl; */

        // total error, detected error, undetected error
        float total_error = 0, detected_error = 0, undetected_error = 0;
        float p_theory = (c_err*(((1-p1_err)*p1_err*(1-p2))+(p1_err*(1-p2)*p2)+(p1_err*p2*p1_err)))+((1-c_err)*((p2*(1-p1_err)*p1_err)+(p2*p1_err*p2)+((1-p2)*p2*(1-p1_err))+((1-p2)*(1-p2)*(1-p2))));
        //float p_theory = (c*(((1-p1)*p1*(1-p2))+(p1*(1-p2)*p2)+(p1*p2*p1)))+((1-c)*((p2*(1-p1)*p1)+(p2*p1*p2)+((1-p2)*p2*(1-p1))+((1-p2)*(1-p2)*(1-p2))));

        for (int i = 0; i < N+(N/3); i += 4){
                if((bin_par[i] != bin_r[i])||(bin_par[i+1] != bin_r[i+1])||(bin_par[i+2] != bin_r[i+2])||(bin_par[i+3] != bin_r[i+3])){
                        ++total_error;
                }
                if((bin_r[i]^bin_r[i+1]^bin_r[i+2]^bin_r[i+3])==1){
                        ++detected_error;
                }
        }
        undetected_error = total_error - detected_error;

        float p_total_error = total_error/(N/3);
        float p_detected_error = detected_error/(N/3);
        float p_undetected_error = undetected_error/(N/3);
        cout << "total error = " << total_error << endl;
        cout << "detected error = " << detected_error << endl;
        cout << endl;
        cout << "undetected error = " << undetected_error << endl;
        cout << "probability of total error = " << p_total_error << endl;
        cout << "probability of detected error = " << p_detected_error << endl;
        cout << "probability of undetected error = " << p_undetected_error << endl;
        cout << "theory = " << p_theory << endl;

        return 0;
}

0 Comments

Markov Information Binary Sequences Based on Piecewise Linear Chaotic Maps

25/1/2021

0 Comments

0. Note

This is the third assignment from my Masters Applied Digital Information Theory Course which has never been published anywhere and I, as the author and copyright holder, license this assignment customized CC-BY-SA where anyone can share, copy, republish, and sell on condition to state my name as the author and notify that the original and open version available here.

1. Introduction

On the first assignment we produced a chaotic sequence based skew tent map by showing that output sequence is uncontrollable as on the chaos theory. A large sequence produced by skew tent map is uniformly distributed. On the second assignment we produce a memoryless binary sequence based on the first assignment's skew tent map based chaotic sequence. The probability of 0, 1, 00, 01, 10, 11, and the Markov chain is analyze. Finally the entropy is calculated based on the critical points of each data and find the correlation between the entropy and expected compression ratio. This time the same method on assignment 2 is used but change the assignment 1 of not using skew tent map but piecewise linear map.

2. Piecewise Linear Chaotic Map

The design procedure of Markov Source we choose 4 values p1, and p2 based on Figure 1. Then can obtain the value c (steady state probability) with the formula c=P(0)=P2/(P1+P2), and then we can find the slope a=1/(1-(p1+p2)). The limitation here is we cannot choose the value that satisfy p1+p2 = 1. We are now ready to design the chaotic map. Basic knowledge on line equation is necessary here the one that refers to the equation y = ax + d where a is the slope that we calculated. There will be 3 lines and at least a positive and negative must be use. Each line we calculate its slope. For Figure 2 we calculate slope a = (y2 – y1)/(x2 – x1). For a=(c-0)/(c-c1)from point x,y of (c1,0) and (c,c). From the equation we can define c1=c-c/a. There's also another slope for a=(1-c)/(c2-c)from point (c,c) and (c2,1) which then we can define c2=c+(1-c)/a. With the first line as negative slope the length proportion of c1:d1 = 1:1-c thus d1 = c1(1-c), and for the third line also negative slope 1-c2:1-d2 = 1:c which we can define d2 = 1+(1-c)c. That's almost all the equation we need, next is to find slope a1 and a2.

For both figure the method to find a1 and a3 is the same which is by using 2 points (x1,y1) and (x2,y2) with calculation slope = (y2 – y1)/(x2 – x1). We use point (d1,c) and (c1,0) for a1. a1=(0-c)/(c1-d1), as for a3 we use (c2,1) and (d2,c) a3=(c-1)/(d2-c2). Finally we can form each line y1, y2, and y3, using equation y – y1 = a(x – x1), but for the map y is regarded as t (it'll be t = a(x-x1) + y1). We then use the following equation to generate the chaotic sequence of p1+p2 < 1.

t = (a1(x-d1))+c for (0⩽x < c1)

t = a(x-c1) for (c1⩽x < c2)

t= a3(x-c2)+1 for (c2⩽x < 1)

For p1+p2 < 1 on the other hand have to change some equation to do the slope a is negative.

On Figure 3 we change one slope for it to be positive, and here we chose a3. Since the slope a2 changes to negative the equation c1 and c2 changes as well, a = (y2 – y1)/(x2 – x1) a=(c-1)/(c-c1)from point x,y of (c1,1) and (c,c). From the equation we can define c1=c-(c-1)/a. C2 changes as well a=(0-c)/(c2-c) from point (c2,0) and (c,c) which then we can define c2=c-c/a. The slope on a1 is still negative, so no changes for d1, but third line we change to positive slope 1-c2:1-d2 = 1:1-c which we can define d2 = 1-(1-c2)(1-c). The last change is on a3=(c-0)/(d2-dc) using point (c2,0) and (d2,c). Not to forget a changes slop recently so t had to be modified based on t = a(x-x1)+y1, the equation then becomes:

t = (a1(x-d1))+c for (0⩽x < c1)

t = a(x-c1)+1 for (c1⩽x < c2)

t = a3(x-c2) for (c2⩽x < 1)

Now we can generate the chaotic sequence on Figure 4. We can see that for p1+p2 < 1 seems more periodic. Lastly on this section we would like to show that the distribution is uniform on Figure 5.

Figure 4a. Generated chaotic sequence of p1 = 0.8 p2 = 0.1 and p1 = 0.1 p2 = 0.8

Figure 4b. Generated chaotic sequence of p1 = 0.5 p2 = 0.6 and p1 = 0.9 p2 = 0.8

Figure 5a. Uniform distribution of p1 = 0.1 p2 = 0.8 N = 1000000

Figure 5b. Uniform distribution of p1 =0.9 p2 = 0.8 N = 1000000

3. Binary Sequences

After that we do the same as assignment 2, generating the binary sequences and counting the 0s and 1s. The result below are as the theory where P(0)=c, P(1)=1-c, P(0|0)=1-p1, P(0|1)=p1, P(1|0)=p2, P(1|1)=1-p2, P(00)=P(0|0)*P(0), P(01)=P(0|1)*P(1), P(10)=P(1|0)*P(1), P(11)=P(1|1)*P(1).

P1 = 0.1p2 = 0.8	Theory	Practice	P1 = 0.8p2 = 0.1	Theory	Practice
0s	-	888925	0s	-	110631
1s	-	111076	1s	-	889370
00s	-	800154	00s	-	21997
01s	-	88770	01s	-	88634
10s	-	88770	10s	-	88634
11s	-	22306	11s	-	800735
P(0)	0.888889	0.888924	P(0)	0.111111	0.110631
P(1)	0.111111	0.111076	P(1)	0.888889	0.889369
P(00)	0.800000	0.800153	P(00)	0.022222	0.021997
P(01)	0.088889	0.088770	P(01)	0.088889	0.088634
P(10)	0.088889	0.088770	P(10)	0.088889	0.088634
P(11)	0.022222	0.022306	P(11)	0.800000	0.800734
P(0\|0)	0.900000	0.900137	P(0\|0)	0.200000	0.198832
P(0\|1)	0.800000	0.799183	P(0\|1)	0.100000	0.099659
P(1\|0)	0.100000	0.099862	P(1\|0)	0.800000	0.801168
P(1\|1)	0.200000	0.200817	P(1\|1)	0.900000	0.900340
Entrophy	0.497099	0.496884	Entrophy	0.497099	0.495759
Filesize (Byte)	1,000,000		Filesize (Byte)	1,000,000
Compressed File	100296		Compressed File	100037
Compression Rate	0.1		Compression Rate	0.1
P1 = 0.5p2 = 0.6	Theory	Practice	P1 = 0.9p2 = 0.8	Theory	Practice
0s	-	544416	0s	-	529516
1s	-	455585	1s	-	470485
00s	-	271392	00s	-	106222
01s	-	273024	01s	-	423294
10s	-	273024	10s	-	423293
11s	-	182561	11s	-	47191
P(0)	0.545455	0.544415	P(0)	0.529412	0.529515
P(1)	0.454545	0.455585	P(1)	0.470588	0.470485
P(00)	0.272727	0.271392	P(00)	0.105882	0.106222
P(01)	0.272727	0.273024	P(01)	0.423529	0.423294
P(10)	0.272727	0.273023	P(10)	0.423529	0.423293
P(11)	0.181818	0.182561	P(11)	0.047059	0.047191
P(0\|0)	0.500000	0.498501	P(0\|0)	0.200000	0.200602
P(0\|1)	0.600000	0.599282	P(0\|1)	0.900000	0.899697
P(1\|0)	0.500000	0.501497	P(1\|0)	0.800000	0.799396
P(1\|1)	0.400000	0.400718	P(1\|1)	0.100000	0.100303
Entropy	0.986796	0.986953	Entropy	0.602901	0.604017
Filesize (Byte)	1,000,000		Filesize (Byte)	1,000,000
Compressed File	159550		Compressed File	110189
Compression Rate	0.16		Compression Rate	0.11

We also perform entropy calculation of the generated binary sequence. We chose to compress the file into format “.tar.gz” one of famous compression in Linux, but this time we use the reversed formula of the second assignment for the compression rate CompressionRate=CompressedFile/OriginalFile thus got the reversed graph, although the meaning is still the same. The lower the compression rate the greater the compressed file, thus higher entropy limits the how far a file can be compressed as on Figure 6.

4. Conclusion

Just as the second assignment the probability of 0s and 1s generated matched the theory. We use reversed equation for compression rate and the as expected the graph become backward thought it is the same thing that lower entropy allows greater compression. The difference in this assignment is that we used piecewise linear chaotic binary sequence which is more complex than skew tent map but allows various map design. This opens possibility to produce different kinds of sequences.

5. Source Code

The source code again is written in Octave and Matlab type language. The script this time is manual so better edit the script and change the values of you want to use it. Next time I might consider uploading the program to available online.

close all
clear
clc

x = 0:.001:1;

p1 = 0.9; p2 = 0.8;
c = p2/(p1+p2);
a = 1/(1-(p1+p2));

if p1+p2 < 1 %positive slope
 c1 = c-(c/a);
 c2 = c+((1-c)/a );
 d1 = c1*(1-c); %(we chose negative slope)
 d2 = 1-((1-c2)*c); %(we chose negative slope)
 
 a1 = -c/(c1-d1); %slope a = y2 - y1 / x2 - x1 (we chose negative)
 a2 = a; %positive slope
 a3 = (c-1)/(d2-c2); % (we chose negative slope)
 
 i = 0;
 
 for i = 1:length(x)
  if x(i) >= 0 && x(i) < c1
   t(i) = (a1*(x(i)-d1))+c;
  elseif x(i) >= c1 && x(i) < c2
   t(i)  = a2*(x(i)-c1);
  else
   t(i) = (a3*(x(i)-c2))+1;
  end
 end
 figure
 plot(x,x,x,t,0,c,c,0,d1,0,c1,0,c2,0,d2,0);
 grid on;
 %title('p1 = 0.1 and p2 = 0.8');
 xlabel('x');
 ylabel('t');
 %legend('reference', 'plot', 'c', 'c', 'd1', 'c1', 'c2', 'd2');
 ylim([0 1]);
 
 N = 1000000;
 X(1) = 0.3;
 
 for i = 1:N
  if X(i) >= 0 && X(i) < c1
   X(i+1) = (a1*(X(i)-d1))+c;
  elseif X(i) >= c1 && X(i) < c2
   X(i+1)  = a2*(X(i)-c1);
  else
   X(i+1) = (a3*(X(i)-c2))+1;
  end
 end

 figure
 plot(0:length(X)-1,X);

 figure
 hist(X,x,length(x));
 %title('p1=0.1 p2=0.8 N=1000000');
 xlim([0 1]);
 ylim([0 2]);
 
 P0_theory = c;
 P1_theory = 1-c;
 P1l0_theory = p1;
 P0l1_theory = p2;
 P0l0_theory = 1-p1;
 P1l1_theory = 1-p2;
 P01_theory = P0l1_theory*P1_theory;
 P10_theory = P1l0_theory*P0_theory;
 P00_theory = P0l0_theory*P0_theory;
 P11_theory = P1l1_theory*P1_theory;
 H_theory = ((p2/(p1+p2))*((-p1*log2(p1))-((1-p1)*log2(1-p1)))) + ((p1/(p1+p2))*((-p2*log2(p2))-((1-p2)*log2(1-p2))));
 
 fprintf('P(0) in theory is %f\n', P0_theory);
 fprintf('P(1) in theory is %f\n', P1_theory);
 fprintf('P(00) in theory is %f\n', P00_theory);
 fprintf('P(01) in theory is %f\n', P01_theory);
 fprintf('P(10) in theory is %f\n', P10_theory);
 fprintf('P(11) in theory is %f\n', P11_theory);
 fprintf('P(0|0) in theory is %f\n', P0l0_theory);  
 fprintf('P(0|1) in theory is %f\n', P0l1_theory);
 fprintf('P(1|0) in theory is %f\n', P1l0_theory);
 fprintf('P(1|1) in theory is %f\n', P1l1_theory);  
 fprintf('Entropy in theory is %f\n\n', H_theory);
 t = c;
 binary = X >= t;
 save("binary_sequence.dat", "binary");
 
 P0_practical = P1_practical = P00_practical = P01_practical = P10_practical = P11_practical = 0;
 
 for i = 1:length(binary)
  if binary(i) == 0
   P0_practical += 1;
  else
   P1_practical += 1;
  end
  
  if i == length(binary)
   break;
  end
  
  if binary(i) == 0 && binary(i+1) == 0
   P00_practical += 1;
  elseif binary(i) == 0 && binary(i+1) == 1
   P01_practical += 1;
  elseif binary(i) == 1 && binary(i+1) == 0
   P10_practical += 1;
  else
   P11_practical += 1;
  end
 end
 
 P0l0_practical = ((P00_practical/length(binary))/(P0_practical/length(binary)));
 P0l1_practical = ((P01_practical/length(binary))/(P1_practical/length(binary)));
 P1l0_practical = ((P10_practical/length(binary))/(P0_practical/length(binary)));
 P1l1_practical = ((P11_practical/length(binary))/(P1_practical/length(binary)));
 H_pratical = ((P0l1_practical/(P1l0_practical+P0l1_practical))*((-P1l0_practical*log2(P1l0_practical))-((P0l0_practical)*log2(P0l0_practical)))) + ((P1l0_practical/(P1l0_practical+P0l1_practical))*((-P0l1_practical*log2(P0l1_practical))-((P1l1_practical)*log2(P1l1_practical))));
 
 fprintf('The number of 0s = %d, P(0) in practice is %f\n', P0_practical, P0_practical/length(binary));
 fprintf('The number of 1s = %d, P(1) in practice is %f\n', P1_practical, P1_practical/length(binary));
 fprintf('The number of 00s = %d, P(00) in practice is %f\n', P00_practical, P00_practical/length(binary));
 fprintf('The number of 01s = %d, P(01) in practice is %f\n', P01_practical, P01_practical/length(binary));
 fprintf('The number of 10s = %d, P(10) in practice is %f\n', P10_practical, P10_practical/length(binary));
 fprintf('The number of 11s = %d, P(11) in practice is %f\n', P11_practical, P11_practical/length(binary));
 fprintf('P(0|0) in practice is %f\n', P0l0_practical);  
 fprintf('P(0|1) in practice is %f\n', P0l1_practical);
 fprintf('P(1|0) in practice is %f\n', P1l0_practical);
 fprintf('P(1|1) in practice is %f\n', P1l1_practical);
 fprintf('Entropy in practice is %f\n\n', H_pratical);
 
elseif p1+p2 > 1 % negative lope
 c1 = c-((c-1)/a);
 c2 = c-(c/a);

 d1 = c1*(1-c); % we chose negative slope
 d2 = 1-((1-c2)*(1-c)); % we chose positive slope

 a1 = -c/(c1-d1); %slope a = y2 - y1 / x2 - x1 (we chose negative)
 a2 = a; % negative lope
 a3 = c/(d2-c2); %(we chose negative)

 for i = 1:length(x)
  if x(i) >= 0 && x(i) < c1
   t(i) = (a1*(x(i)-d1))+c;
  elseif x(i) >= c1 && x(i) < c2
   t(i)  =(a2*(x(i)-c1))+1;
  else
   t(i) = a3*(x(i)-c2);
  end
 end
 figure
 plot(x,x,x,t,0,c,c,0,d1,0,c1,0,c2,0,d2,0);
 grid on;
 %title('p1 = 0.9 and p2 = 0.8');
 xlabel('x');
 ylabel('t');
 %legend('reference', 'plot', 'c', 'c', 'd1', 'c1', 'c2', 'd2');
 ylim([0 1]);
 
 N = 1000000;
 X(1) = 0.3;

 for i = 1:N
  if X(i) >= 0 && X(i) < c1
   X(i+1) = (a1*(X(i)-d1))+c;
  elseif X(i) >= c1 && X(i) < c2
    X(i+1)  =(a2*(X(i)-c1))+1;
  else
     X(i+1) = a3*(X(i)-c2);
  end
 end

 figure
 plot(0:length(X)-1,X);

 figure
 hist(X,x,length(x));
 %title('p1=0.9 p2=0.8 N=1000000');
 xlim([0 1]);
 ylim([0 2]);
  
 P0_theory = c;
 P1_theory = 1-c;
 P1l0_theory = p1;
 P0l1_theory = p2;
 P0l0_theory = 1-p1;
 P1l1_theory = 1-p2;
 P01_theory = P0l1_theory*P1_theory;
 P10_theory = P1l0_theory*P0_theory;
 P00_theory = P0l0_theory*P0_theory;
 P11_theory = P1l1_theory*P1_theory;
 H_theory = ((p2/(p1+p2))*((-p1*log2(p1))-((1-p1)*log2(1-p1)))) + ((p1/(p1+p2))*((-p2*log2(p2))-((1-p2)*log2(1-p2))));
 
 fprintf('P(0) in theory is %f\n', P0_theory);
 fprintf('P(1) in theory is %f\n', P1_theory);
 fprintf('P(00) in theory is %f\n', P00_theory);
 fprintf('P(01) in theory is %f\n', P01_theory);
 fprintf('P(10) in theory is %f\n', P10_theory);
 fprintf('P(11) in theory is %f\n', P11_theory);
 fprintf('P(0|0) in theory is %f\n', P0l0_theory);  
 fprintf('P(0|1) in theory is %f\n', P0l1_theory);
 fprintf('P(1|0) in theory is %f\n', P1l0_theory);
 fprintf('P(1|1) in theory is %f\n', P1l1_theory);  
 fprintf('Entropy in theory is %f\n\n', H_theory);
 t = c;
 binary = X >= t;
 save("binary_sequence.dat", "binary");
 
 P0_practical = P1_practical = P00_practical = P01_practical = P10_practical = P11_practical = 0;
 
 for i = 1:length(binary)
  if binary(i) == 0
   P0_practical += 1;
  else
   P1_practical += 1;
  end
  
  if i == length(binary)
   break;
  end
  
  if binary(i) == 0 && binary(i+1) == 0
   P00_practical += 1;
  elseif binary(i) == 0 && binary(i+1) == 1
   P01_practical += 1;
  elseif binary(i) == 1 && binary(i+1) == 0
   P10_practical += 1;
  else
   P11_practical += 1;
  end
 end
 
 P0l0_practical = ((P00_practical/length(binary))/(P0_practical/length(binary)));
 P0l1_practical = ((P01_practical/length(binary))/(P1_practical/length(binary)));
 P1l0_practical = ((P10_practical/length(binary))/(P0_practical/length(binary)));
 P1l1_practical = ((P11_practical/length(binary))/(P1_practical/length(binary)));
 H_pratical = ((P0l1_practical/(P1l0_practical+P0l1_practical))*((-P1l0_practical*log2(P1l0_practical))-((P0l0_practical)*log2(P0l0_practical)))) + ((P1l0_practical/(P1l0_practical+P0l1_practical))*((-P0l1_practical*log2(P0l1_practical))-((P1l1_practical)*log2(P1l1_practical))));
 
 fprintf('The number of 0s = %d, P(0) in practice is %f\n', P0_practical, P0_practical/length(binary));
 fprintf('The number of 1s = %d, P(1) in practice is %f\n', P1_practical, P1_practical/length(binary));
 fprintf('The number of 00s = %d, P(00) in practice is %f\n', P00_practical, P00_practical/length(binary));
 fprintf('The number of 01s = %d, P(01) in practice is %f\n', P01_practical, P01_practical/length(binary));
 fprintf('The number of 10s = %d, P(10) in practice is %f\n', P10_practical, P10_practical/length(binary));
 fprintf('The number of 11s = %d, P(11) in practice is %f\n', P11_practical, P11_practical/length(binary));
 fprintf('P(0|0) in practice is %f\n', P0l0_practical);  
 fprintf('P(0|1) in practice is %f\n', P0l1_practical);
 fprintf('P(1|0) in practice is %f\n', P1l0_practical);
 fprintf('P(1|1) in practice is %f\n', P1l1_practical);
 fprintf('Entropy in practice is %f\n\n', H_pratical);
else
 fprintf('you cannot do this');
end

0 Comments

Chaotic and Memoryless Binary Sequences Based on Skew Tent Maps

24/1/2021

0 Comments

0. Note

This is the second assignment from my Masters Applied Digital Information Theory Course which has never been published anywhere and I, as the author and copyright holder, license this assignment customized CC-BY-SA where anyone can share, copy, republish, and sell on condition to state my name as the author and notify that the original and open version available here.

1. Introduction

On the previous assignment we generate a chaotic sequence based on skew tent maps, and this time we generate a binary sequence (either '0' or '1'). On this occasion we generate the chaotic binary sequence based on the threshold function.

bin = 0 if (x < c)

bin = 1 if (x ≥ c)

When a sequence value 'x' is less than critical point 'c' the binary value will be '0' and when a sequence value 'x' is equal or greater to critical point 'c' the binary value will be '1'. For example the critical value is set as 'c' = 0.4 and chaotic sequence 'x' = [0.750000 0.416667 0.972222 0.046296 0.115741 0.289352 0.723380], the binary sequence will be 'bin' = [1 1 1 0 0 0 1] as Figure 1.

2. Probability of binary sequence

Using the chaotic sequence based on skew tent map to generate binary sequence we compute the probability the sequence value will be '0' or '1' as 'P(0) = c' and 'P(1) = 1-c'. Using the skew tent map we can compute 'P(00) = c x c', 'P(01) = c(1-c)', 'P(10) = (1-c)c', and 'P(11) = (1-c)(1-c)'. On Markov's chain the probability that '0' will remain '0' is 'P(0|0) = c', '0' will become '1' is 'P(1|0) = 1-c', and so-on 'P(0|1) = c', 'P(1|1) = 1-c'.

We continue the assignment using the previous assignment to generate the binary sequence and calculate the probability of '0' and '1' theoretically and the actual number of '0' and '1' on the binary sequence generated. We used the initial value 'x(1) = 0.3' and trials of 'c = 0.1, 0.2, 0.301, 0.4, 0.6, 0.7, 0.8, 0.9'. The total sequence generated is 2000000 values (2 Millions). The result is on Table 1.

Table 1. Result of theoritical calculation and actual

Probability	Theory	Actual	Theory	Actual	Theory	Actual	Theory	Actual
P(0)	0.1	0.100183	0.2	0.199925	0.301	0.300855	0.4	0.399797
P(1)	0.9	0.899817	0.8	0.800076	0.699	0.699146	0.6	0.600203
P(00)	0.01	0.010015	0.4	0.040114	0.091	0.090433	0.16	0.159818
P(01)	0.09	0.090169	0.16	0.159811	0.21	0.210422	0.24	0.239979
P(10)	0.09	0.090169	0.16	0.159811	0.21	0.210422	0.24	0.239979
P(11)	0.81	0.809649	0.64	0.640265	0.489	0.488724	0.36	0.360225
P(0\|0)	0.1	0.999962	0.2	0.200656	0.301	0.300585	0.4	0.399757
P(0\|1)	0.1	0.100208	0.2	0.199744	0.301	0.30097	0.4	0.39983
P(1\|0)	0.9	0.900038	0.8	0.799354	0.699	0.699413	0.6	0.600252
P(1\|1)	0.9	0.899792	0.8	0.800256	0.699	0.69903	0.6	0.600171
Entropy	0.46899559	0.46957542	0.72192809	0.72177695	0.88250986	0.88233261	0.97095059	0.97083172
Filesize Original (bits)	2000000		2000000		2000000		2000000
Filesize Compressed (bits)	136892		221013		278698		312480
Compression Ratio	14.61005756		9.049241447		7.176226597		6.400409626

Probability	Theory	Actual	Theory	Actual	Theory	Actual	Theory	Actual
P(0)	0.6	0.599315	0.7	0.700161	0.8	0.800442	0.9	0.899851
P(1)	0.4	0.400685	0.3	0.299839	0.2	0.199559	0.1	0.10015
P(00)	0.36	0.359091	0.49	0.490351	0.64	0.6406	0.81	0.809735
P(01)	0.24	0.240225	0.21	0.209811	0.16	0.159842	0.9	0.090115
P(10)	0.24	0.240224	0.21	0.20981	0.16	0.159842	0.9	0.090115
P(11)	0.16	0.160461	0.09	0.09003	0.04	0.039718	0.01	0.010035
P(0\|0)	0.6	0.599168	0.7	0.70034	0.8	0.800307	0.9	0.899855
P(0\|1)	0.6	0.599535	0.7	0.699744	0.8	0.800976	0.9	0.899805
P(1\|0)	0.4	0.400831	0.3	0.29966	0.2	0.199692	0.1	0.100144
P(1\|1)	0.4	0.400467	0.3	0.300258	0.2	0.199027	0.1	0.1002
Entropy	0.97095059	0.97134988	0.8812909	0.88109401	0.72192809	0.7210441	0.46899559	0.46946961
Filesize Original (bits)	2000000		2000000		2000000		2000000
Filesize Compressed (bits)	312428		278355		220769		136833
Compression Ratio	6.4014749		7.185069426		9.059242919		14.61635717

While the theoretical probability was calculated based on the formula, we count how much '0's and '1's in the sequence consist of 2 Millions binary values. For example using 'c = 0.4' we got 799594 '0's and 1200406 '1's in the 2 Millions sequence. So the actual probability of '0' is '799594/2000000 = 0.399797' and '1' is '1200406/2000000 = 0.600203'. For '00's is 319635, '01's is 479958, '10' is 479958, and '11' is 720449. Everything else is on Table 1, and actual data matched the theory. For Entropy and compression ratio is discussed on the next section.

3. Entropy vs Compression Ratio

On this binary sequence we can calculate the entropy which is how much important information contained. The higher the entropy (more important information) the lower the compression ratio (the least it can be compressed). Based on Table 1 we also calculated entropy of the sequence with the following formula.

Entropy = -P(1)log₂P(1) - P(0)log₂P(0)

On this experiment the generated 2 million binary sequence is saved into a '.dat' file. The raw file for all 'c' value will equal to 2MB. Here we chose to compress the '.dat' file into '.tar.bz2' format which is a common compression method in Linux. Finally we can plot the entropy to the compression ratio on Figure 2 which is as stated in the theory that the compression value increases with lower entropy.

4. When t ≠ c is not memoryless

When generating the binary sequence uses the threshold function bin = 0 (x < t) @ 1 ( x ≥ t), on above section it's automatically adjust that t = c to produce a memoryless binary sequence. One of the ways to show that the binary sequence is memoryless is that it fulfills Markov's chain on Figure 3, other than through the Bernoulli trials and independent and identically distributed (iid). We see that on table 2 that the probability is not balance, the probability of turning and remains '0' should be the same, same goes for the probability of turning to 1.

Table 2. Data of t ≠ c

x = 0.3	c = 0.4	x = 0.3	t = 0.1
P(0\|0)	0.399757	P(0\|0)	0.396616
P(0\|1)	0.39983	P(0\|1)	0.066858
P(1\|0)	0.600252	P(1\|0)	0.603384
P(1\|1)	0.600171	P(1\|1)	0.933142

5. Conclusion

Using the chaotic sequence generated by skew tent map we can generate the random binary sequence with the probability of '0's and '1's computable. The result above shows that the theoretical probability of '0's, '1's, '00's, '01's, '10's, '11's, and the Markov's chain where the probability of '0' will remain '0', will turn to '1', '1' will remain '1', or turn to '0' matches from the actual binary sequence generated. The theory is true to the actual. On the second case where we compare the entropy to capability of the compression, the greater the entropy the less the compression ratio. We found that the sequence is not memoryless when t ≠ c because it does not fulfill the Markov's Chain.

6. Source Code

The script is created in Ruby language, use Ruby to run.

#!/usr/bin/ruby -w

x = c = Array.new;
binary_sequence = Array.new;
$P0 = $P1 = $P00 = $P01 = $P10 = $P11 = $P0l0 = $P0l1 = $P1l0 = $P1l1 = 0;

print "Input initial value x[1] from 0 ~ 1: ";
x[1] = gets.chomp.to_f;
print "\nInput critical point c[1] from 0 ~ 1: ";
c = gets.chomp.to_f;
print "\nInput number of sequence N: ";
N = gets.chomp.to_f;

for n in 1..N
 if x[n] >= 0 and x[n] < c
  x[n+1] = x[n]/c;
 elsif x[n] >= c and x[n] <= 1
  x[n+1] = (1-x[n])/(1-c);
 else
  print "x must be from 0 ~ 1";
 end
end

puts "P(0)_theory = c = #{c}";
puts "P(1)_theory = 1-c = #{1-c}";
puts "P(00)_theory = c*c = #{c*c}";
puts "P(01)_theory = c(1-c) = #{c*(1-c)}";
puts "P(10)_theory = (1-c)c = #{(1-c)*c}";
puts "P(11)_theory = (1-c)*(1-c) = #{(1-c)*(1-c)}";
puts "P(0|0)_theory = c = #{c}";
puts "P(0|1)_theory = c = #{c}";
puts "P(1|0)_theory = 1-c = #{1-c}";
puts "P(1|1)_theory = 1-c = #{1-c}";
puts "";

file = File.new("binary_sequence.dat", "w");

for n in 1..N
 if x[n] < c
  binary_sequence[n] = 0;
  $P0 += 1;
 elsif x[n] >= c
  binary_sequence[n] = 1;
  $P1 += 1;
 else
  print "something is wrong";
 end
#print binary_sequence[n];
file.syswrite(binary_sequence[n]);
end

P0_actual = $P0/N.to_f;
P1_actual = $P1/N.to_f;

for n in 1..N
 if binary_sequence[n] == 0 and binary_sequence[n+1] == 0
  $P00 += 1;
 elsif binary_sequence[n] == 0 and binary_sequence[n+1] == 1
  $P01 += 1;
 elsif binary_sequence[n] == 1 and binary_sequence[n+1] == 0
  $P10 += 1;
 else
  $P11 += 1;
 end
end

P00_actual = $P00/N.to_f;
P01_actual = $P01/N.to_f;
P10_actual = $P10/N.to_f;
P11_actual = $P11/N.to_f;

P0l0_actual = P00_actual/P0_actual;
P0l1_actual = P01_actual/P1_actual;
P1l0_actual = P10_actual/P0_actual;
P1l1_actual = P11_actual/P1_actual;

puts "P(0)_actual = #{P0_actual}";
puts "P(1)_actual = #{P1_actual}";
puts "P(00)_actual = #{P00_actual}";
puts "P(01)_actual = #{P01_actual}";
puts "P(10)_actual = #{P10_actual}";
puts "P(11)_actual = #{P11_actual}";
puts "P(0|0)_actual = #{P0l0_actual}";
puts "P(0|1)_actual = #{P0l1_actual}";
puts "P(1|0)_actual = #{P1l0_actual}";
puts "P(1|1)_actual = #{P1l1_actual}";
puts "";

puts Entropy = ((-P1_actual)*(Math.log2(P1_actual)))-((P0_actual)*(Math.log2(P0_actual)));

puts "Total of '0' is #{$P0}";
puts "Total of '1' is #{$P1}";
puts "Total of '00' is #{$P00}";
puts "Total of '01' is #{$P01}";
puts "Total of '10' is #{$P10}";
puts "Total of '11' is #{$P11}";

0 Comments

Chaotic Real-Valued Sequences By Skew Tent Map

23/1/2021

0 Comments

0. Note

This is the first assignment from my Masters Applied Digital Information Theory Course which has never been published anywhere and I, as the author and copyright holder, license this assignment customized CC-BY-SA where anyone can share, copy, republish, and sell on condition to state my name as the author and notify that the original and open version available here.

1. Introduction

The chaos theory is a field of study in mathematics that studies the behaviour of dynamical system. Rober L. Devaney stated a system can be chaotic if it is sensitive to initial value, topologically mixing, and have a dense periodic orbit. The theory was summarized by Edward Lorenz. Although the system was highly determined by the initial value, in the end the sequence is unpredictable. Chaos exist in many natural system such as the climate and whether. In the field of computer science, it's applied to generate random values.

2. Tent Map

The tent map can be formulated as t = x/c for 0 ≤ x < c and t = (1-x)/(1-c) for c ≤ x ≤ 1 where:

c = critical point

x = initial value

t = tent map (next value for sequence)

For example c = 0.5 with x from 0 to 1:

Figure 1 is based on the equation that the value would range from 0 to 1, and when “x” reached the critical point, the value of “t” will equals to 1. It is up to us to decide the critical point, as in Figure 2 shows if “c” equals to 0.2. Another information is if “x” equals to 0 or 1 the end result will be 0, thus using this value is not recommended.

3. Chaotic Sequence

In some areas the tent map equation is used to generate chaotic sequence, here t(n) = x(n+1). The equation would turn into x(n+1) = (x(n))/c for 0 ≤ x(n) < c and x(n+1) = (1-x(n))/(1-c) for c ≤ x(n) ≤ 1. Why the equation is stated differently? So the value of x(n+1) will never exceed 1. For example if “c = 0.4” and “x = 0.5” and use the first equation “x(n)/c = 0.5/0.4 = 1.25”. That won't do so we use “1-x(n)/1-c = 1 - 0.5 / 1 - 0.4 = 0.5/0.6 = 0.833”. Another example “c = 0.7” and “x = 0.4” which we can't use the second equation “1-x(n)/1-c = 1 - 0.4 / 1 - 0.7 = 0.6/0.3 = 2” but we use “x(n)/c = 0.7/0.4 = 0.571”.

As stated in the chaos theory the next sequence “x(n+1)” is highly dependable on the initial value “x(n)” (x(2) depends on x(1), x(3) depends on x(2), etc), as we plot the sequences it will looked unpredictable.

3.1 For “x” equals to 0 and 1, and “c” equals to 0.5

image x(1) = 0 and x(1) = 1 — Figure 3a. image x(1) = 0

Figure 3 is only plotted to the 10th “n” because the result is obvious. For x(1) (initial) equals to 0, x(2) = 0/c = 0 and for x(1) x(2) = (1-1)/(1-c) = 0/(1-c) = 0. Once the value is zero, the next value will always be zero, and for x(1) equals to c x(2) = c/c = 1, x(3) = (1-1)/(1-c) = 0. When “x” reaches critical point “c” it will result to 1, and once the next value “x(n+1)” equals to 1 the next value “x(n+2)” will result to 0, and once it reaches to 0 the next value will always be 0. With the explanation above we can see that it's not recommended to use a critical point “c” equals to 0.5. In Figure 4b when “c = 0.5” it's susceptible for “x” in reaching “c”. On the 54th “n” “x(n) = c” and “x(n+1) = 1”, then the next result will always be 0.

Figure 4a. Tent map x(1) = 0.2 and c = 0.5

Figure 4b. Sequence x(1) = 0.2 and c = 0.5

3.2 For “c” equals to 0.6 and x = 0.3 and 0.8

Figure 5a shows that when “c” equals to 0.6, “t” will have the same value when “x” equals to 0.3 and 0.8. Thus the sequence generated at Figure 5b will be the same. At the same time it is shown the sequence will be continuous.

Figure 5a. Tent Map of c = 0.6 and x = 0.3 and 0.8

Figure 5b. Sequence x(1) = 0.3 and 0.8 (no difference)

3.3 Sensitivity to Initial Value

The chaos theory stated that it is sensitive to initial value, just a slight change can totally change the whole sequence. For example “c = 0.4” and we'll try “x” with initial value of 0.7, 0.71, 0.72, 0.73 on Figure 6 and “x” with initial value of 0.7111, 0.71111, 0.711111, 0.7111111 on Figure 7.

Figure 6a. Graph c = 0.4 and x(1) = 0.7, 0.71, 0.72, 0.73 tent map

Figure 6b. Graph c = 0.4 and x(1) = 0.7, 0.71, 0.72, 0.73 up to 10 sequence

Figure 6c. Graph c = 0.4 and x(1) = 0.7, 0.71, 0.72, 0.73 up to 100 sequence

Figure 6d. Graph c = 0.4 and x(1) = 0.7, 0.71, 0.72, 0.73 up to 1000 sequence

On Figure 7 we tried even more extreme which we plot of each initial value with a difference of 0.0001, 0.00001, 0.000001, and 0.0000001. There seems to be no difference on up to the 10th sequence, but the sequences finally deviated on the 15th “n” sequence for 0.7111 and 0.71111, then followed up by the other initial values that have smaller difference.

Figure 7a. Graph c = 0.4 and x(1) = 0.7111, 0.71111, 0.711111, 0.7111111 tent map

Figure 7b. Graph c = 0.4 and x(1) = 0.7111, 0.71111, 0.711111, 0.7111111 up to 10 sequence

Figure 7c. Graph c = 0.4 and x(1) = 0.7111, 0.71111, 0.711111, 0.7111111 up to 100 sequence

Figure 7d. Graph c = 0.4 and x(1) = 0.7111, 0.71111, 0.711111, 0.7111111 up to 1000 sequence

Even with small difference it's still unpredictable on the 100th sequence, let alone the 1000th sequence. This proofs the sensitivity to initial values (where the “x” starts).

3.4 Distributions of the sequences

On this section we will see the distribution of value from 0 to 1, specifically from 0, 0.01, 0.02 ~ 1. Only 0 to 1 because the sequence is formulated to not go below 0 and go above 1. The histogram on Figure 8 shows the distribution of value with critical point “c” of 0.4 and initial value “x(1)” of 0.7. This time we produce a sequence as much as “n = 1000000” (million) (the more the sequence the better). Plotting that much data cannot be seen in one graph, in other word it's not visible, but with histogram we can see what and how much the values contained in the sequence.

Figure 8. Data count on x(1) = 0.7, c = 0.4, n = 1000000

Figure 8 shows that there is around 10000 data with a value of 0.1, 0.2, and so on. The hist() function works by rounding, for example the value of 0.1111 will be rounded to 0.1, and the value of 0.15 rounded to 0.2. Then the value is counted up (how many 0.1s there is) and a distrubution histogram was graphed. Finally it can be said that the distribution of data is uniformed since the amount of data for each value is almost the same.

4. Conclusion

We can conclude that the chaos sequence is formed by previous value like a memory system. Since it's very sensitive to initial value, the further the sequence becomes more unpredictable. The theory is a simple application of the natural system for example the weather. We can predict the weather maybe for a month, beyond that it's likely miss prediction. The course of whether is determined by its starting point, the wrong initial value will lead to the wrong prediction. On the other hand the more accurate the initial value and the formula, the longer the validity of the prediction. Since the unpredictable outcome of this chaos theory, in computer it can be also applied for creating random values. On this simulation the distribution of the skew tent to the chaotic sequence, we found it to be uniformed.

5. Source Code

The source code is written in “m file” that could run on Matlab or Octave alike. It is a function which can be run as “stcsfp(xo,c,N)” where “xo = initial value”, “c = critical point”, and “N = number of sequence”. For example the plotted graph above we run by “stcsfp(0.7,0.4,1000000)”, but we can delete function if it seems inconvenient by deleting the 1st line and use it as regular script. The graphs above are done by few modifications of the code, but here on Code 1 resides the pure source code.

function t = stcsfp(xo,c,N)

% === TENT MAP === %

X = 0:.1:1;

for n = 1:11
 if X(n) >= 0 && X(n) < c
  T(n) = X(n)/c;
 elseif X(n) >= c && X(n) <=1
  T(n) = (1-X(n))/(1-c);
 else
  printf("x initial must be from 0 to 1");
 end
end

% === MAIN CALCULATION === %
x(1) = xo;

for n = 1:N
 if x(n) >= 0 && x(n) < c
  t(n) = x(n)/c;
  x(n+1) = t(n);
 elseif x(n) >= c && x(n) <=1
  t(n) = (1-x(n))/(1-c);
  x(n+1) = t(n);
 else
  printf("x initial must be from 0 to 1");
 end
end

%Plot Tent Map%
figure
plot(X, T, xo, t(1));
title("Tent Map");
xlabel("X");
ylabel("T");
%legend("fill this in")

%Plot Sequence%
figure
plot(t);
title("Sequence Generated");
xlabel("n");
ylabel("t(n) or x(n+1)");
ylim([-0.1 1.1]);
%legend(["fill this in"]);
%xlim([1 20])

%Plot Histogram%
figure
hist(t, 0:.01:1);
title("Distribution");
xlabel("Value");
ylabel("Count");
xlim([-0.1 1.1]);

Code 1. Skew Tent Chaotic Sequence Program

Mirrors

0 Comments

Mendukung Media Sosial Kripto Torum Seperti Duta Besar dengan Menanggapi Posting Terkait Lainnya

23/1/2021

1 Comment

platform interaction — Di artikel saya sebelumnya, saya menulis tentang hal-hal sederhana yang siapa pun dapat melakukan untuk mendukung Torum di platform lain yang mengikuti dan menyukai. Sementara saya juga menyebutkan secara teknis tentang komentar dan posting menggunakan tagar dan sebutan, di sini saya akan menguraikan lebih banyak lagi layaknya sebagai duta besar. Berbeda dengan hal-hal sederhana, dukungan semacam ini membutuhkan usaha.

Mencari dan Menanggapi Posting Terkait Torum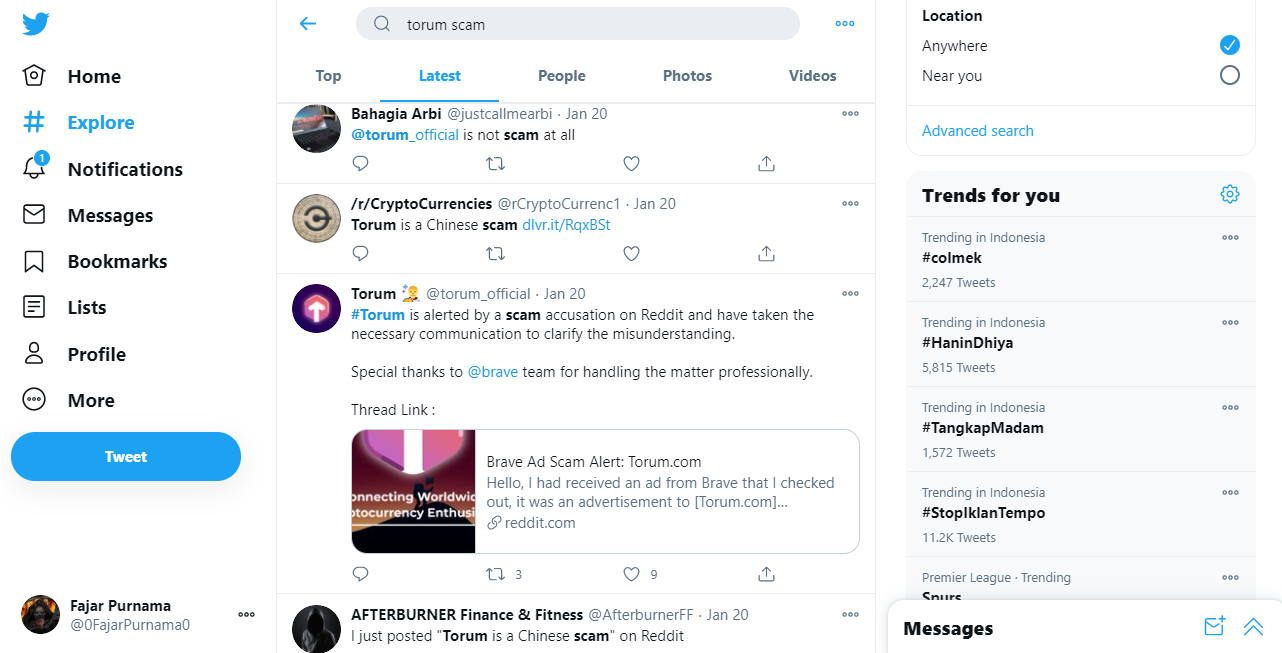

torum twitter search — Hampir semua platform memiliki bilah pencarian di mana kita dapat mencari setidaknya posting apa pun dengan kata torum. Akan lebih bagus juga jika orang menggunakan hashtag seperti #Torum dan di Tweeter ada orang yang menggunakan simbol mata uang seperti $XTM. Cari mereka dan tanggapi mereka.

torum scam accusation — Meskipun menanggapi semuanya adalah hal terbaik untuk dilakukan, tetapi saya ragu ada orang yang memiliki ketekunan untuk melakukan itu. Karena itu, usahakan yang penting dulu. Misalnya, tuduhan penipuan ke Torum perlu segera diperhatikan karena merusak reputasi Torum. Tidak masalah jika semua orang di dunia memeriksa fakta terlebih dahulu sebelum memberikan penilaian, tetapi kebanyakan orang tidak rela repot-repot untuk melakukan ketekunan yang dihormati tersebut dan hanya percaya apa pun yang dikatakan orang-orang terlebih dahulu. Dengan kata lain, kebanyakan orang malas untuk berpikir sendiri. Misalnya, "Mengapa Torum itu Scam?", jawabannya "Karena beberapa orang mengatakan demikian", dan pola pikir ini dipersenjatai oleh para pembenci untuk memfitnah Torum di mana orang tidak ingin repot-repot memeriksa platform dimana lebih mudah untuk mempercayai rumor. Oleh karena itu, jika kami para pendukung tidak merespon, orang akan percaya bahwa Torum adalah scam. Ada banyak pendekatan untuk menanggapinya:

Menjadi Pendukung hingga Pejuang

Kebalikan dari pembenci di mana Anda membela apa pun yang terjadi dan mengekspresikan perasaan Anda hanya karena Anda mendukung Torum:

"Saya sudah lama di Torum dan saya memiliki pengalaman yang menyenangkan."
"Saya sangat menyukai Torum, jadi sangat sedih mendengar pernyataan Anda."
"Saya sering berhubungan dengan tim dan mereka adalah orang-orang yang baik dan pekerja keras."

Selain bertahan, Anda dapat menyerang lawan:

"Pernyataan kebencian Anda seolah-olah hanya untuk mencari perhatian."
"Kamu bodoh karena menyebutnya scam tanpa penelitian yang tepat, seharusnya kamu bisa lebih pintar."
"Gara-gara pembenci sepertimu yang terus bikin proyek-proyek hancur."

Menjadi Pihak ke-3 yang Obyektif

Saya melihat banyak pendukung memberikan pernyataan sederhana seperti yang saya tunjukkan sebelumnya tetapi secara pribadi saya tidak merekomendasinya karena tidak peduli seberapa banyak Anda mendukung, Anda bukanlah pendiri atau pemilik, Anda adalah Anda. Alasan lainnya adalah fakta dan kebenaran selalu menang dalam jangka panjang. Tidak seperti menjadi suporter, Anda harus bertindak seperti robot tanpa emosi dan berbicara hanya berdasarkan salah satu atau semua tentang data, logika, pendapat Anda sendiri, dll.

Ada banyak bot. Bagaimana "hanya bot" terkait dengan "scam"? Apakah para pendiri menggunakan bot? Para pendiri hanya menyediakan platform, pengguna lain yang menggunakan bot. Meski begitu, adakah bukti yang mendukung klaim tersebut? Kalaupun ada bukti, apa kaitannya dengan "scam"?
Pra-penjualan XTM adalah scam yang tidak diketahui. Meskipun pernyataan ini tidak bisa sepenuhnya salah tetapi tidak ada penjelasannya. Mengapa ini scam? Bagaimana bisa "jelas" jika tidak ada penjelasan sama sekali? Hanya satu kalimat, itu saja, jadi pendapat saya adalah "informasi yang buruk". Tunggu, tapi repot untuk menulis semua detailnya. Sayangnya, detail harus diberikan. Ini adalah tuduhan langsung dan bukan hanya tweet atau artikel acak. Tuduhan ini merusak reputasi Torum, oleh karena itu penuduh harus bertanggung jawab dengan memberikan detail atau ini tidak akan ada bedanya dengan "cyber bullying".
Mengumpulkan profil wajah, nomor telepon, dan email ...... terus kenapa? Sekali lagi tidak ada penjelasan dan apa hubungannya dengan "scam".
Jangan ragu untuk memverifikasi klaim saya. Apakah Anda malas sehingga perlu meminta orang lain untuk memverifikasi?

xtm beta only holder — Tuduhan pendek sebagian besar berbahaya seperti di masa lalu tanpa dasar menuduh banyak wanita sebagai penyihir. Detail itu penting dan yang terbaik dari semuanya adalah kritik yang membangun. Meskipun saya adalah duta Torum tetapi saya tidak takut untuk mengakui:

Ya, ada banyak bot di Torum. Namun, saya memberikan saran, dorongan karena saya juga pendukung, dan screenshot. Saya menulis sebuah artikel mengatakan bahwa Torum juga dibombardir oleh spam dan saya menginformasikan pendapat saya tentang bagaimana platform lain seperti Steemit & Hive, Uptrennd, dan read.cash menanganinya.
Daripada tuduhan tidak berdasar bahwa pra-penjualan XTM adalah scam yang jelas-jelas terlihat, saya lebih suka memberikan bukti terkait kekhawatiran. Jika Anda berpikir bahwa saya tidak akan berani bahwa saya hanyalah anak anjing yang mengibas-ngibaskan ekor saya, maka Anda salah. Dalam artikel yang sama tentang spam di Torum, saya memberikan bukti dari Etherscan bahwa hanya ada satu alamat yang menyimpan semua XTM. Artinya XTM saat ini adalah kustodian yang hanya dapat digunakan di dalam sistem dan saya mengerti jika investor tidak akan berinvestasi hanya berdasarkan alasan ini. Jika para pendiri mengeluh tentang saya membagikan bukti ini, saya tidak akan berpikir dua kali untuk membantah karena itu adalah fakta yang saya tunjukkan. Namun, para pendiri telah dewasa dan agak setuju dengan asumsi saya bahwa mereka perlu menyelesaikan sistem terlebih dahulu sebelum mendistribusikan.
Tidak ada hal seperti mengumpulkan profil wajah yang berlaku di semua platform media sosial. Kami tidak pernah fokus untuk mengunggah gambar apa pun dan tahukah Anda, kami bisa membiarkannya kosong. Karenanya, ini hanyalah klaim kekanak-kanakan yang menyalahkan kecanggungan kita sendiri karena mengunggah profil wajah. Untuk email dan nomor telepon, itu benar jadi jangan bergabung dengan Torum jika Anda tidak ingin memberikannya.

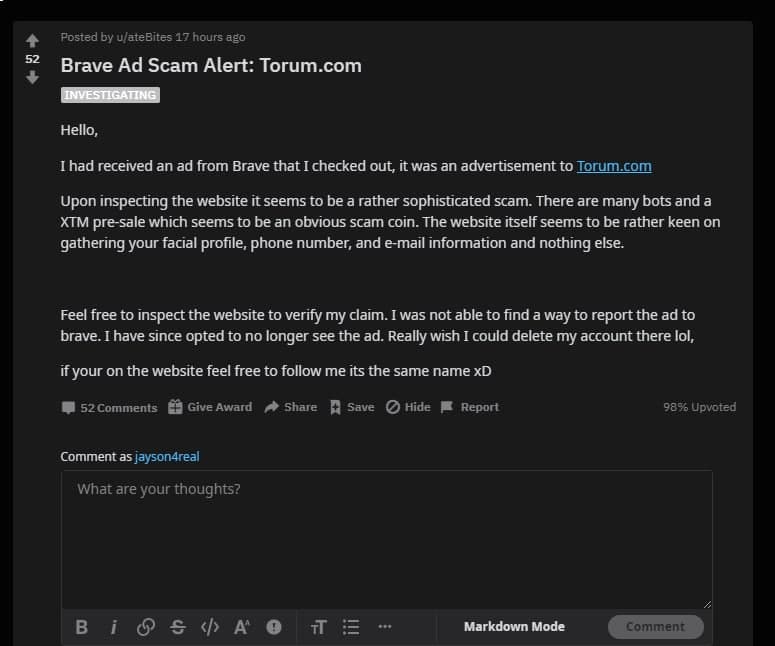
Menjadi Penjahat ke-3

Meskipun orang tidak percaya setiap saat ketika saya mengakui bahwa saya memiliki temperamen buruk tetapi mereka tidak mengeluh ketika saya mengakui bahwa saya sarkastik dan saya meminta maaf. Ini berbeda dengan menjadi pendukung yang menyerang atau pihak ketiga yang objektif yang mengkritik tetapi lebih seperti area abu-abu di mana Anda ingin menunjukkan taring Anda pada penuduh atau menunjukkan taring Anda kepada kedua belah pihak hanya untuk diri Anda sendiri. Berikut adalah utas lain:

Torum is a Chinese scam from r/torumtech

Saya tidak akan menyangkal jika komentar saya dituduh mencari perhatian tetapi secara pribadi saya hanya ingin mengungkapkan perasaan saya:

> Torum adalah penipuan Cina

Tapi Anda bilang itu orang Malaysia, bukan Cina. Saya membagikan alamat lengkap kantor pusat mereka di artikel Publish0x saya.

> Semua kripto hilang. Hati-hati dengan skema pompa dari Malaysia ini.

Apakah Anda membeli XTM? Jika Anda tidak "membeli", Anda tidak boleh membuat klaim seperti itu.

> Penipuan China yang tidak diatur lainnya di mana Anda akan dilarang jika tidak disukai oleh komunis di belakang platform ini. Tentu saja mereka akan menyangkal.

Saya tidak setuju dengan yang terakhir. Pernyataan tidak akurat dimana bukan komunis tetapi komunitas yang ketat. Saya tidak berpikir mereka akan menyangkal karena saya mendengar mereka berencana memberikan kekuatan penuh kepada komunitas. Jika mayoritas komunitas tidak menyukai konten Anda meskipun konten tersebut sah di mana laporan besar-besaran dibuat, Anda akan diblokir. Bahkan saya diancam akan diblokir hanya dengan menulis pernyataan ini. Saya bahkan diberitahu tahu bahwa jika komunitas tidak menyukai konten non-kripto saya, maka saya pun tidak terkecuali.

Dan satu hal lagi, perusahaan mereka adalah publik di Malaysia. Jika menurut Anda mereka tidak diatur atau bahkan lebih buruk lagi, scam, mengapa tidak menghubungi pihak berwenang Malaysia saja?

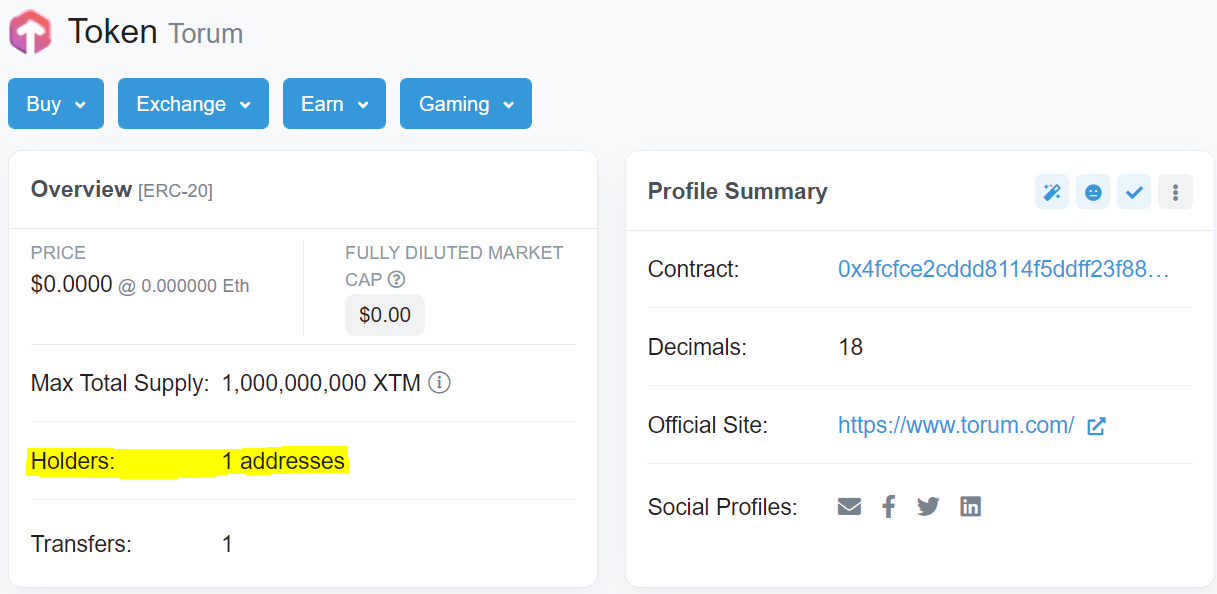
Menjadi Seorang Pelapor

NB, Saya minta maaf kepada penuduh yang membaca komentar kasar di atas. Ini hanyalah contoh bagaimana orang dapat mendekati dan saya tahu bahwa Anda telah menyelesaikan masalah Anda di antara mereka ketika saya membaca komentar terakhir Anda dan sebaliknya komentar saya untuk utas Anda ada di bawah:

Card

Ini adalah peran favorit saya karena saya suka membimbing orang dan membiarkan mereka berpikir sendiri. Di sini Anda tidak menyerang atau membela atau melibatkan emosi apa pun. Anda hanya memberikan informasi dan tidak lebih dari itu. Misalnya, di bawah ini komentar saya tentang tuduhan scam:

Halo, Anda dan semua orang dapat membeli tiket dan pergi ke alamat ini dan memberi tahu mereka secara langsung mengapa menurut Anda itu adalah penipuan:

Alamat: Pusat Perdagangan, 43-2-4, Jalan Kampar Barat 3, Taman Kampar Barat, 31900 Kampar, Perak, Malaysia

Nomor Telpon: +6054684400

Kode Plus: 84CH+85 Kampar, Perak, Malaysia

Halaman Web: torum.com

Jam Buka:

Minggu 12–8PM

Senin 10AM–7:30PM

Selasa 10AM–7:30PM

Rabu 10AM–7:30PM

Kamis 10AM–7:30PM

Jumat 10AM–7:30PM

Sabtu 12–8PM

Jika Anda ingin informasi lebih lanjut tentang para pendiri, silakan periksa artikel saya di Publish0x dan jika Anda ingin menjangkau mereka di platform lain, baca artikel saya yang lain.

Duta Besar Mana Yang Ditugasi Untuk Pekerjaan Ini?

torum ambassador 0fajarpurnama0 — Humas Twitter, Komunitas Telegram, Acara Membangun Komunitas, dan Membangun Komunitas Klan. Tunggu, apakah saya juga sedang mencari perhatian dengan menulis artikel ini? Tidak, tanpa rasa malu saya akan mengatakan bahwa ini untuk mengisi kuota mingguan saya sebagai Duta Penulisan Konten @0fajarpurnama0. Apakah Anda punya satu atau dua kata? Ucapkan langsung ke Torum: https://www.torum.com/signup?referral_code=0fajarpurnama0.

1 Comment

<<Previous

Crypto & Technology Blog

1. Cyber Attacks Can Come From Based on This Lecture

2. International Standard Organization Information Security Management

1. Kernel Vulnerabilities

2. Server Program and CGI Vulnerabilities

3. Common Steps For Handling Previous Vulnerabilities

4. Some of My Comments and Experiences

1. Mitigation

2. Evasion

3. Treatment

4. Last Resort

1. Network Consists of Clients and Servers

2. There Are Many Bots on The Network

3. Popular Hacking Methods

4. My Prior Knowledge About Penetration Testing

0. Note

1. Introduction

2. Memoryless Errors (Skew Tent Map)

3. Markov-type Errors (PWL Map)

4. Results

5. Source Code

0. Note

1. Introduction

2. Skew Tent Map

3. PWL Map

4. Summary

5. Source Code

0. Note

1. Introduction

2. Piecewise Linear Chaotic Map

3. Binary Sequences

4. Conclusion

5. Source Code

0. Note

1. Introduction

2. Probability of binary sequence

3. Entropy vs Compression Ratio

4. When t ≠ c is not memoryless

5. Conclusion

6. Source Code

0. Note

1. Introduction

2. Tent Map

3. Chaotic Sequence

3.1 For “x” equals to 0 and 1, and “c” equals to 0.5

3.2 For “c” equals to 0.6 and x = 0.3 and 0.8

3.3 Sensitivity to Initial Value

3.4 Distributions of the sequences

4. Conclusion

5. Source Code

Mirrors

Mencari dan Menanggapi Posting Terkait Torum

Menjadi Pendukung hingga Pejuang

Menjadi Pihak ke-3 yang Obyektif

Menjadi Penjahat ke-3

Menjadi Seorang Pelapor

Duta Besar Mana Yang Ditugasi Untuk Pekerjaan Ini?

Archives

Categories